6.1 Area between two curves

1
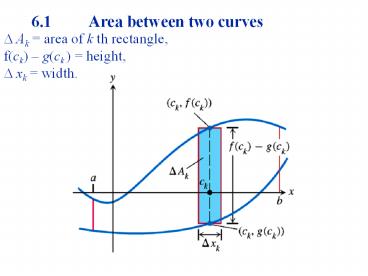
6.1 Area between two curves
??Ak area of k th rectangle,?f(ck) g(ck )
height, ??xk width.
2
Find the area of the region between the curves
Figure 4.23 When the formula for a bounding
curve changes, the area integral changes to
match. (Example 5)
3
Section 6.2 Figure 5
Approximating the volume of a sphere with radius 1
(b) Using 10 disks, V 4.2097
(c) Using 20 disks, V 4.1940
(a) Using 5 disks, V 4.2726
A
4
6. 2 Volumes Solid of revolution
Figure 5.6 The region (a) and solid (b) in
Example 4.
y f(x) is rotated about x-axis on a,b. Find
the volume of the solid generated. A
cross-sectional slice is a circle and a slice is
a disk.
5
Volumes Solid of revolution
Figure 5.6 The region (a) and solid (b) in
Example 4.
6
Volumes by disk-y axis rotation
Find the volume of the solid generated by
revolving a region between the y-axis and the
curve x 2/y from y 1 to y 4.
7
Find the volume of the solid generated by
revolving a region between the y-axis and the
curve x 2/y from y 1 to 4.
8
Washers
Figure 5.10 The cross sections of the solid of
revolution generated here are washers, not disks,
so the integral ????A(x) dx leads to a slightly
different formula.
If the region revolved does not border on or
cross the axis of revolution, the solid has a
hole in it. The cross sections perpendicular to
the axis are washers.
b a
V Outside Volume Inside Volume
9
. The region bounded by the curve y x2 1 and
the line y -x 3 is revolved about the x-axis
to generate a solid. Find the volume of the solid
of revolution.
10
The inner and outer radii of the washer swept out
by one slice. Outer radius R - x 3 and the
inner radius r x2 1
11
The inner and outer radii of the washer swept out
by one slice. Outer radius R - x 3 and the
inner radius r x2 1
Find the limits of integration by finding the
x-coordinates of the points of intersection.
x2 1 - x 3
x2 x 20
( x 2 )(x 1) 0
x -2 x 1
12
Calculation of volume
Outer radius R - x 3 and the inner radius r
x2 1
13
y-axis rotation
The region bounded by the parabola y x2 and the
line y 2x in the first quadrant is revolved
about the y-axis to generate a solid. Find the
volume of the solid.
Drawing indicates a dy integration so solve each
equation for x as a function of y
Set to find y limits of integration
y 0 and y 4 are limits
14
The washer swept out by one slice perpendicular
to the y-axis.
15
calculation
The region bounded by the parabola y x2 and the
line y 2x in the first quadrant is revolved
about the y-axis to generate a solid. Find the
volume of the solid.
16
6. 3 Cylindrical Shells
Figure 5.17 Cutting the solid into thin
cylindrical slices, working from the inside out.
Each slice occurs at some xk between 0 and 3 and
has thickness ? x. (Example 1)
Used to find volume of a solid of revolution by
summing volumes of thin cylindrical shells or
sleeves or tree rings.
17
volume of a shell
Imagine cutting and unrolling a cylindrical shell
to get a (nearly) flat rectangular solid. Its
volume is approximately V length ? height ?
thickness.
)
Vshell 2?(radius)(height)(thickness)
18
problem
The region enclosed by the x-axis and the
parabola y f(x) 3x x2 is revolved about
the y axis. Find the volume of the solid of
revolution.
Vshell 2?(radius)(height)(thickness)
19
The shell swept out by the kth rectangle.
Notice this axis or revolution is parallel to the
red rectangle drawn.
20
problem
21
The region, shell dimensions, and interval of
integration in
22
The shell swept out by the rectangle in.
23
Summary-Volumes-which method is best
Axis of rotation
24
Lengths of Plane curves
Find the length of the arc formed by
u 1 4x du 4dx du/4 dx
25
Follow the link to the slide. Then click on the
figure to play the animation.
A
Figure 6.2.5
Figure 6.3.7
Figure 6.2.12
26
Section 6.3 Figures 3, 4
Volumes by Cylindrical Shells
27
Computer-generated picture of the solid in
Example 9
Section 1 / Figure 1
A