Session 6 Daily Check - PowerPoint PPT Presentation
1 / 32
Title:
Session 6 Daily Check
Description:
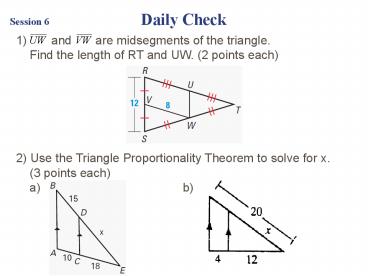
Session 6 Daily Check and are midsegments of the triangle. Find the length of RT and UW. (2 points each) 2) Use the Triangle Proportionality Theorem to ... – PowerPoint PPT presentation
Number of Views:107
Avg rating:3.0/5.0
Title: Session 6 Daily Check
1
Session 6 Daily Check
- and are midsegments of the triangle.
- Find the length of RT and UW. (2 points each)
- 2) Use the Triangle Proportionality Theorem to
solve for x. - (3 points each)
- a) b)
2
Homework Review
3
CCGPS Analytic GeometryDay 6 (8-21-13)
UNIT QUESTION How do I prove geometric theorems
involving lines, angles, triangles and
parallelograms? Standards MCC9-12.G.SRT.1-5,
MCC9-12.A.CO.6-13 Todays Question What does it
mean for two triangles to be congruent? Standard
MCC9-12.G.SRT5, CO.7-8
4
5-4 Congruent Triangles
Congruent triangles have congruent sides and
congruent angles. The parts of congruent
triangles that match are called corresponding
parts.
5
Complete each congruence statement.
B
C
A
D
F
DEF
E
6
Complete each congruence statement.
ECD
7
Complete each congruence statement.
GTK
8
CPCTC
Corresponding Parts of Congruent Triangles are
Congruent
9
Fill in the blanks
?O
- If ?CAT ? ?DOG, then ?A ? ___
- because ________.
CPCTC
10
Fill in the blanks
- If ?FJH ? ?QRS, then ___
- and ?F ? ___ because _______.
?Q
CPCTC
CPCTC
?B
11
Congruence of Triangles
12
Overlapping sides are congruent in each triangle
by the REFLEXIVE property
Alt Int Angles are congruent given parallel lines
Vertical Angles are congruent
13
Before we startlets get a few things straight
INCLUDED ANGLE
14
Side-Side-Side (SSS) Congruence Postulate
4
4
5
5
6
6
All Three sides in one triangle are congruent to
all three sides in the other triangle
15
Side-Angle-Side (SAS) Congruence Postulate
Two sides and the INCLUDED angle
16
Ex 1
DFE
UVW
by ____
SSS
17
Determine whether the triangles are congruent.
If they are, write a congruency statement
explaining why they are congruent.
Ex 2
?RST ? ?YZX by SSS
18
Determine whether the triangles are congruent.
If they are, write a congruency statement
explaining why they are congruent.
Ex 3
Not congruent. Not enough Information to Tell
19
Determine whether the triangles are congruent.
If they are, write a congruency statement
explaining why they are congruent.
Ex 4
P
R
Q
S
?PQS ? ?PRS by SAS
20
Determine whether the triangles are congruent.
If they are, write a congruency statement
explaining why they are congruent.
Ex 5
P
S
U
Q
R
T
?PQR ? ?STU by SSS
21
Determine whether the triangles are congruent.
If they are, write a congruency statement
explaining why they are congruent.
Ex 6
M
P
R
Q
N
Not congruent. Not enough Information to Tell
22
Before we startlets get a few things straight
INCLUDED SIDE
23
Angle-Side-Angle (ASA) Congruence Postulate
Two angles and the INCLUDED side
24
Angle-Angle-Side (AAS) Congruence Postulate
Two Angles and One Side that is NOT included
25
SSS SAS ASA AAS
NO BAD WORDS
Your Only Ways To Prove Triangles Are Congruent
26
Ex 1
DEF
NLM
by ____
ASA
27
Ex 2
What other pair of angles needs to be marked so
that the two triangles are congruent by AAS?
28
Ex 3
What other pair of angles needs to be marked so
that the two triangles are congruent by ASA?
29
Determine whether each pair of triangles is
congruent by SSS, SAS, ASA, or AAS. If it is not
possible to prove that they are congruent, write
not possible.
Ex 4
?GIH ? ?JIK by AAS
30
Determine if whether each pair of triangles is
congruent by SSS, SAS, ASA, or AAS. If it is not
possible to prove that they are congruent, write
not possible.
Ex 5
?ABC ? ?EDC by ASA
31
Determine if whether each pair of triangles is
congruent by SSS, SAS, ASA, or AAS. If it is not
possible to prove that they are congruent, write
not possible.
E
Ex 6
A
C
B
D
?ACB ? ?ECD by SAS
32
Determine if whether each pair of triangles is
congruent by SSS, SAS, ASA, or AAS. If it is not
possible to prove that they are congruent, write
not possible.
Ex 7
J
T
L
K
V
U
Not possible
33
HW/CW-PRACTICE on Notes Page
34
HW- More Congruent Triangles WS