Random Rough Surface Scattering

1
Random Rough Surface Scattering
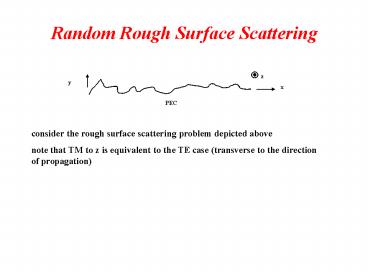
consider the rough surface scattering problem
depicted above note that TM to z is equivalent to
the TE case (transverse to the direction of
propagation)
2
Integral Equation
on the PEC surface
3
Integral Equation
where f y(x)
4
Tapered Incident Field
the rough surface has a finite length, is
truncated at xL/2 the incident field cannot be
a uniform plane wave, otherwise, diffraction from
the end points may be significant the incident
field is chosen as a tapered wave that reads
g is the tapering parameter
5
Long Surface is Required for Near Grazing
Incidence
near grazing incidence, the RHS would not be
close to zero g and therefore L must be very
large for near grazing incidence
6
TE-to-z or TM (to the Direction of Propagation)
Note that we can use the MFIE for the thin shell
problem since a tapered wave is used, as the
other side of the surface has zero fields.
7
Difference between TE and TM Case
the former one has a symmetric impedance matrix
while that of the latter one is
non-symmetric when the surface is large, the
number of unknowns will be large and the matrix
solution time will be long we have developed a
banded matrix iterative approach to solve a large
matrix for the one-dimensional rough surface (a
two-dimensional scattering) problem 
8
Spatial Domain Methods
one disadvantage of the spectral domain is that
it requires numerical integration of infinite
extend spatial domain Greens functions are not
readily available for layered media with
applications in microstrip antennas and
high-frequency circuits methods have been
developed to circumvent this difficulty we will
discuss the complex image method in conjunction
with the Rao-Wilton-Glisson triangular
discretization the mixed-potential integral
equation (MPIE)
9
Microstrip Structures
has arbitrary surface conductor geometry ground
plane and substrate extend to infinity in the
transverse direction and the space above the
dielectric is unbounded the substrate is
homogeneous and isotropic, but not necessarily
lossless the upper conductor and ground plane
have zero resistivity, and the upper conductor is
infinitely thin our goal is to compute the
surface current distribution from which other
parameters can be extracted
10
Mixed-Potential Integral Equation (MPIE)
it has weaker singularities in its Greens
functions than the EFIE, rendering more quickly
convergent solutions
11
Rao-Wilton-Glisson (RWG) Triangular Basis
Functions
O
these functions overlap, and each plate can be
part of up to three different basis functions
12
Rao-Wilton-Glisson (RWG) Triangular Basis
Functions
13
Rao-Wilton-Glisson (RWG) Triangular Basis
Functions
the current flows from plate to
, with maximum current across the common edge,
zero current at the isolated vertices and
, and no currents with components normal to
the other four sides the weighting in the current
representation is such that the current normal to
the common edge is continuous across that edge,
and hence, no fictitious charge singularities
arise when the continuity equation is applied to
the basis function, the charge density is a
constant equal to and on
each plate and the total charge is zero
14
Method of Moments
15
Simplications
many identical integrations will be
performed considerable computational effort is
saved by evaluating and storing the scalar
potential integral for all plate combinations and
recalling these results as needed in evaluating
the matrix elements the same cannot be said of
the integral for the vector potential, whose
integrand evaluated over a particular source
triangle depends on the identity of the isolated
vertex and, hence, the basis function to which
the triangle is assigned
16
Simplications
where is set alternately to x, yand
1 the basis function dependence is removed from
the integrals and reintroduced in the evaluation
of Zmn through a weighted sum of these three for
each plate combination, a total of four scalar
integrals are evaluated and later recalled in
constructing the elements in impedance matrix
Z the excitation vector is given by
17
Spectral-Domain Greens Function
no closed-form expressions for Ga and Gq in the
spatial domain, but they can be represented in
closed-form in the spectral domain
Wave numbers kzo and kr are the vertical and
radial components of the free-space propagation
constant ko in the cylindrical system RTE and RTM
are the reflection coefficients at the interface
of TE and TM plane waves incident on the
substrate with ground plane
18
Spatial Greens Function through Transformation
the spatial-domain Greens functions can then be
expressed as an inverse Hankel-transform of the
spectral counterparts, commonly referred to as
Sommerfeld integrals
Approximate analytic expressions exist for the
evaluation of the Hankel-transform for r in the
near and far fields a technique developed by
Prof. Fang Dagang of the Nanjing University of
Science and Technology and improved by Prof. Y.
L. Chow allows efficient evaluation in all regions
19
Complex Image Method
the Sommerfeld integral is divided into three
contributions 1) quasi-dynamic images, 2)
surface waves, and 3) complex images the first
two contributions, which dominate respectively in
the near-and far-field, are extracted from RTE
and RTM and handled analytically using the
Sommerfeld Identity what remains in RTE and RTM
is relatively well behaved and exhibits
exponential decay for sufficiently large values
of kr the remainder can be accurately
approximated with a short series of exponentials
terms, which are interpreted as complex images
20
Complex Image Method
the exponents of the expansion are computed using
Pronys method or the matrix pencil method and
the term weights then obtained through a
least-square fit the inverse Hankel-transform of
the exponentials can be performed analytically,
again using the Sommerfeld Identity two to four
expansion terms are appropriate, depending on the
frequency particular care should be taken in
determining the number for expansion terms of Gq
since its contribution in the scalar potential is
a second-order difference arising from the source
pulse-doublet and the testing procedure
21
Efficient Implementation
all elements in the impedance matrix can be
computed from a linear combination of four scalar
integrals evaluated for all source/test plate
combinations the surface integration over the
source plate can be replaced by evaluation of the
integrand at the plate centroid
22
Efficient Implementation
the difference between the distances from the
three vertices of the source plate to the test
plate centroid is under some set maximum level,
say 20, then that approximation is viable it
makes sense to evaluate the Greens functions
with an interpolation table both Ga and Gq
exhibit 1/r and log r singularities, so the table
must begin at some minimum displacement ro
governed by the interpolation scheme, the
dominant 1/r singularity, and a maximum error
criterion, say 1
23
Efficient Implementation
the interactions can be catalogued by stepping
through each plate combination far-interactions
are ignored, as they are too numerous to store
and can be rapidly evaluated through the Ga and
Gq for near interactions, the four scalar
integrals are evaluated and catalogued subsequent
plate combinations are then checked against the
stored interactions and computed only if no
equivalent interactions is available Two plate
interaction integrals are equivalent if the x-
and y-displacements of the test plate centroid
from the source plate vertices are identical
24
Expressions Needed
25
Sommerfeld Identity
26
Use of Sommerfeld Identity
27
Curve Fitting using Complex Exponentials
it is unfortunate that brute force application of
signal processing techniques would not yield
satisfactory results in representing our
functions
28
Quasi-Dynamic Contributions
at very low frequency, , RTE and
Rq can be reduced to the quasi-dynamic form given
by
29
Quasi-Dynamic Contributions
surface-wave contribution dominates in the far
field
30
Surface-Wave Contributions
31
Complete Expressions