Constant returns to scale

1
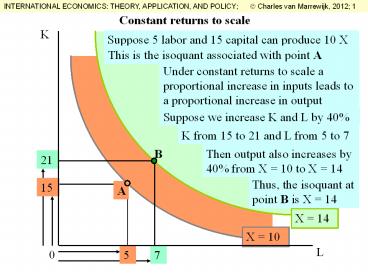
Constant returns to scale
Suppose 5 labor and 15 capital can produce 10 X
This is the isoquant associated with point A
Under constant returns to scale a proportional
increase in inputs leads to a proportional
increase in output
Suppose we increase K and L by 40
K from 15 to 21 and L from 5 to 7
Then output also increases by 40 from X 10 to
X 14
Thus, the isoquant at point B is X 14
2
Constant returns to scale
Increasing the inputs at A with 40 is equivalent
to increasing the length of a line from the
origin through A with 40
This procedure can be repeated for any arbitrary
point on the X10 isoquant here are a few
The X 14 isoquant is a blow-up
radial
3
Constant returns to scale
Under constant returns to scale the isoquants are
radial blow-ups of each other, which implies that
drawing 1 isoquant gives information on all others
For example, that if cost is minized at point A
for X 10, then it is also minimized at the 40
radial blow-up of A (B) for X 14
Thus, the slope of the isoquant at point A is the
same as at point B
4
Constant returns to scale
Since the isoquants are radial blow-ups of one
another and the slope at point A is the same as
the slope at point B cost minimization is simpler.
If we know the cost minimizing input mix for one
isoquant and any ratio of w/r, we also know it
for any other production level.
You only have to multiply the input mix times the
output ratio (we frequently use the isoquant X
1)