Computational grid size

1
1 of 19
Maco-Micro Modeling Simple methods for
incorporating small scale effects into large
scale solidification models Vaughan Voller,
University of Minnesota
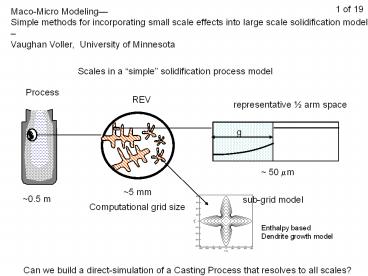
Scales in a simple solidification process model
Computational grid size
Enthalpy based Dendrite growth model
Can we build a direct-simulation of a Casting
Process that resolves to all scales?
2
2 of 19
Scales in Solidification Processes
(after Dantzig)
Can we build a direct-simulation of a Casting
Process that resolves to all scales?
3
3 of 19
Well As it happened not currently Possible
1000 20.6667 Year Moores Law
2055 for tip
Voller and Porte-Agel, JCP 179, 698-703 (2002)
Plotted The three largest MacWasp Grids (number
of nodes) in each volume
4
4 of 19
Scales in Solidification Processes
(after Dantzig)
To handle with current computational Technology
require a Micro-Macro Model
See Rappaz and co-workers
Example a heat and Mass Transfer model Coupled
with a Microsegregation Model
5
5 of 19
Solidification Modeling
Process
REV
representative ½ arm space
solid
g
sub-grid model
50 mm
Micro segregationsegregation and solute
diffusion in arm space
5 mm
0.5 m
Computational grid size
from computation Of these values
need to extract
--
--
--
6
6 of 19
Primary Solidification Solver
g
Transient mass balance
g
model of micro-segregation
Iterative loop
Cl
T
(will need under-relaxation)
Give Liquid Concentrations
equilibrium
7
Micro-segregation Model
7 of 19
liquid concentration due to macro-segregation
alone
½ Arm space of length l takes tf seconds to
solidify
In a small time step new solid forms with lever
rule on concentration
Need an easy to use approximation For
back-diffusion
8
8 of 19
The parameter Model --- Clyne and Kurz,
Ohnaka
9
9 of 19
The Profile Model
Wang and Beckermann
10
10 of 19
Arm-space will increase in dimension with time
Coarsening
This will dilute the concentration in the liquid
fractioncan model be enhancing the


back
diffusion ?
11
11 of 19
Constant Cooling of Binary-Eutectic Alloy With
Initial Concentration C0 1 and Eutectic
Concentration Ceut 5, No Macro segregation
, k 0.1
Use 200 time steps and equally increment 1 lt Cl
lt 5
Calculating the transient value of g from
Remaining Liquid when C 5 is Eutectic Fraction
Parameter or Profile
12
12 of 19
Results are good across a range of conditions
13
13 of 19
Predictions of Eutectic Fraction With constant
cooling
Co 4.9 Ceut 33.2 k 0.16
Comparison with Experiments Sarreal Abbaschian
Met Trans 1986
14
14 of 19
Parabolic solid growth No Second Phase No
Coarsening Use 10,000 equal of Dg C0 1,
k 0.13, a 0.4
Use
To calculate evolving segregation ratio
15
15 of 19
Performance of Models under parabolic growth no
second phase
in last liquid to solidify
Prediction of segregation ratio
(fit exponential through last two time points)
16
My Method of Choice
17
17 of 19
I Have a BIG Computer Why DO I need an REV and a
sub grid model
solid
50 mm
5mm
(about 106 nodes)
.5m
18
18 of 19
Application Inverse Segregation in a binary
alloy
Shrinkage sucks solute rich fluid toward chill
results in a region of ve segregation at chill
100 mm
Fixed temp chill results in a similarity
solution
19
19 of 19
Comparison with Experiments
Ferreira et al Met Trans 2004