LECTURE 2: DIVERGENCE THEOREM, PRESSURE, ARCHIMEDES PRINCIPLE

1
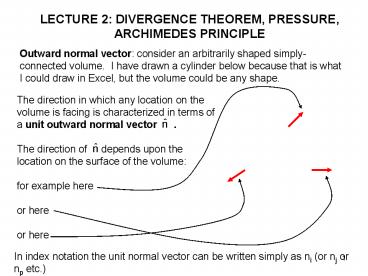
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
Outward normal vector consider an arbitrarily
shaped simply-connected volume. I have drawn a
cylinder below because that is what I could draw
in Excel, but the volume could be any shape.
The direction in which any location on the volume
is facing is characterized in terms of a unit
outward normal vector .
The direction of depends upon the location on
the surface of the volume for example here or
here or here
In index notation the unit normal vector can be
written simply as ni (or nj or np etc.)
2
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
The divergence theorem is a simple example of a
more general integral theorem that comes in many
other flavors. It relates an integral defined
over the surface of a control volume to another
over the internal volume of the control volume
Using the velocity vector as an example, the
standard divergence theorem takes the form
where S denotes the surface of the volume, dA
denotes an element of surface area, V denotes the
volume of the control volume, and dV denotes an
element of volume.
Note that the unit outward normal vector is
denoted as ni in index notation.
3
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
The following integral theorems which are related
to the divergence theorem will also prove useful
in this course
The first of these holds for any scalar
(zeroth-order tensor) A and the second holds for
any matrix (second-order tensor) Aij, but the
examples of pressure and the stress tensor have
been chosen for a reason that will become
apparent before long.
4
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
All of these theorems represent 3-dimensional
analogs of the simple statement that integration
and differentiation are reciprocal operations, or
more specifically
Here we prove the following theorem for a an
infinitesimal rectangular control volume
The control volume has dimensions ?x, ?y and ?z
5
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
Now consider the two faces in the y direction.
On the left face
and on the right face
6
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
Similarly computing the contribution from the
other two faces, it is found that
so establishing the theorem for an infinitesimal
body.
7
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
The stress tensor
contains the normal stresses ?11, ?22 and ?33 and
the shear stresses ?12, ?21, ?13, ?31, ?23 and
?32.
In fluids, the normal stresses ?11, ?22 and ?33
have components associated with pressure that are
all equal to each other. Since a normal stress
is defined as positive for the case of tension,
and since fluids are generally in compression, it
makes sense to change the sign convention and
define these pressure components as
so that p is positive when the fluid is in
compression.
8
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
A fluid can be defined as a state of matter which
cannot withstand a sustained shear stress without
flowing. The flow continues until application of
the shear stress is halted. Thus for a fluid to
be at rest in static equilibrium, all the shear
stresses ?12, ?13, ?23, ?21, ?32 and ?31 must be
vanishing, so that the stress tensor takes the
form
Now why should the three normal stresses be
equal, or equivalently, why should pressure p be
isotropic (the same in every direction)?
9
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
To show why this is the case, we first consider a
fluid at rest (fluid statics, or hydrostatics in
the case of water). Gravity pulls the water
down. But the water does not move because it is
in static balance. Static balance is obtained
when the pressure distribution is just sufficient
to balance gravity.
Consider the illustrated control volume with
height ?z in the vertical direction and area ?A
in the horizontal plane. For simplicity, the
fluid has a free surface, the location of which
is located by the inverted triangle. (The
existence of a free surface is not necessary for
the derivation. In addition, the fluid is
assumed to be incompressible, so that density ?
is (to a high degree of approximation) constant.
?A
?z
z?z
z
10
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
The downward force of gravity acting on the
control volume is given as ?g?z?A.
The pressure force acting on the bottom face is
p(z)?A, and it acts upward. (Remember that a
positive pressure always acts to compress)
The pressure force acting on the top face is
p(z?z)?A, and it acts downward.
For static equilibrium, then, the force balance is
?A
p(z?z)
?z
z?z
z
p(z)
11
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
The relation
or
Is the foundation of the study of fluid statics
of incompressible fluids. It says that pressure
increases linearly downward in the fluid.
But this relation in and of itself is
insufficient to establish that pressure is
isotropic, as it only considers the vertical
direction.
12
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
Now consider the static fluid in the illustrated
volume with a right-triangular cross-section and
angle ?.
The volume has dimensions ?x, ?y and ?z where z
denotes the upward vertical direction.
p3
?z
The pressures acting on the bottom face, left
side face and diagonal face are denoted as p1, p2
and p3, respectively. Note that each pressure
acts inward normal to the face in question.
?
p2
?y
The volume is (1/2)?x?y?z and the weight is
?g(1/2)?x?y?z (which acts only downward.)
?x
p1
The area ?A of the diagonal face is given as
The pressure force on the diagonal face has
components p3?Acos? acting downward and p3?Asin?
acting to the left in the horizontal plane.
13
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
Force balance in the vertical direction
p3
?z
?
p2
In the limit as ?x, ?y and ?z all ? 0 we
obtain the following result at a point
?y
?x
p1
?
14
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
p3
?z
?
p2
?y
?x
p1
?
15
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
Now the angle ? was not specified, so the result
holds for any angle. The result, then, is that
the pressure p at a point is isotropic, or the
same in any direction.
Strictly speaking, the result holds only for
static fluids. But it easily generalizes to
moving fluids. For example, let the fluid be
accelerating in the vertical direction at rate
az. The force balance then generalizes to
or in the limit as ?z ? 0,
16
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
Archimedes theorem states that a body submerged
in a static fluid is buoyed upward by a force
equal to the weight of fluid it displaces. Thus
if the body has volume V and the upward vertical
coordinate is z x3, the buoyant force FBi
acting on the body is
17
LECTURE 2 DIVERGENCE THEOREM, PRESSURE,
ARCHIMEDES PRINCIPLE
Now lets prove Archimedes theorem using the
divergence theorem.
Consider an elemental area dA on the surface of
the body with unit outward normal vector ni.
Since pressure pushes inward, the pressure force
on the elemental area is
ni
dA
p
so establishing the desired result.