Training Data PowerPoint PPT Presentation
1 / 44
Title: Training Data
1
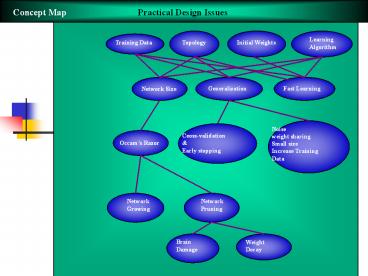
Concept Map
Practical Design Issues
Learning Algorithm
Training Data
Topology
Initial Weights
Fast Learning
Network Size
Generalization
Noise weight sharing Small size Increase
Training Data
Ceoss-validation Early stopping
Occams Razor
Network Growing
Network Pruning
Brain Damage
Weight Decay
2
Concept Map
Fast Learning
BP variants
Cost Function Activation Function
Training Data
No weight Learning For Correctly Classified Patter
ns
?
Normalize Scale Present at Random
Adaptive slope
Momentum
Architecture
Other Minimization Method
Fahlmanns
Modular
Committee
Conjugate Gradient
3
Chapter 4. Designing Training MLPs
- Practical Issues
- Performance f (training data, topology,
initial weights, learning algorithm, . . .) - Training Error,
Net Size, Generalization.
- How to prepare training data, test data ?
- - The training set must contain enough info to
learn the task. - - Eliminate redundancy, maybe by data
clustering. - - Training Set size N gt W/?(N of training
data, W of weights, - e Classification error permitted on
Test data - Generalization error)
4
Ex. Modes of Preparing Training Data for Robot
Control The importance of the training data
for tracking performance can not be
overemphasized. Basically, three modes of
training data selection are considered here. In
the regular mode, the training data are obtained
by tessellating the robots workspace and taking
the grid points as shown in the next page.
However, for better generalization, a sufficient
amount of random training set might be obtained
by observing the light positions in response to
uniformly random Cartesian commands to the robot.
This is the random mode. The best generalization
power is achieved by the semi-random mode which
evenly tessellates the workspace into many cubes,
and chooses a randomly selected training point
within each cube. This mode is essentially a
blend of the regular and the random modes.
5
Training Data Acquisition mode
Regular mode
Random mode
Semi-random mode
6
Fig.10. Comparison of training errors and
generalization errors for random and semi-random
training methods.
7
- Optimal Implementation
- A. Network Size
- Occams Razor
- Any learning machine should be
- sufficiently large to solve a given problem, but
not - larger.
- A scientific model should favor simplicity or
- shave off the fat in the model.
- Occam 14th century British monk
8
a. Network Growing Start with a few / add more
(Ref. Kim, Modified Error BP Adding Neurons
to Hidden Layer, J. of KIEE 92/4)
If E gt ?1 and ?E lt ?2, Add a hidden
node. Use the current weights for existing
weights and small random values for newly added
weights as initial weights for new learning. b.
Network Pruning ? Remove unimportant
connections After brain damage, retrain
the network. ? Improves generalization.
? Weight decay
after each epoch c. Size Reduction by Dim.
Reduction or Sparse Connectivity in Input
Layer e.g. Use 4 random instead of 8 connections
9
(No Transcript)
10
B. Generalization Train (memorize) and
Apply to an Actual
problem (generalize)
Poor
Good
test(O)
test(O)
train(X)
train(X)
Overfitting (due to too many traning samples,
weights) noise
R
X
T Training Data
X Test Data
R'
T
R NN with Good Generalization
R' NN with Poor Generalization
U
11
For good generalization, train with Learning
Subset. Check on validation set. Determine
best structure based on Validation Subset 10 at
every 5-10 iterations. Train further with
the full Training Set. Evaluate on test set.
Statistics of training (validation) data must be
similar to that of test (actual problem)
data. Tradeoff between training error and
generalization !
Stopping Criterion Classification Stop upon
no error
Function Approximation check
12
An Example showing how to prepare the various
data sets to learn an unknown function from data
samples
13
- Other measures to improve generalization.
- Add Noise (1-5 ) to the Training Data or
Weights. - Hard (Soft) Weight Sharing (Using Equal Values
for Groups of Weights) - Can Improve Generalization.
- For fixed training data, the smaller the net the
better the generalization. - Increase the training set to improve
generalization. - For insufficient training data, use leave-one
(some)-out method - Select an example and train the net
without this example, evaluate with
this unused example. - If still does not generalize well, retrain with
the new problem data. - C. Speeding Up Accelerating Convergence
- - Ref. Book by Hertz, AI Expert Magazine 91/7
- To speed up calculation itself
- Reduce Floating Point Ops by Using a Fixed
Point Arithmetic - And Use a Piecewise-Linear approximation for the
sigmoid.
14
Students Questions from 2005
What will happen if more than 5-10 validation
data are used ? Consider 2 industrial assembly
robots for precision jobs made by the same
company with an identical spec. If the same NN is
used for both, then the robots will act
differently. Do we need better generalization
methods to compensate for this difference ? Large
N may increase noisy data. However, wouldnt
large N offset the problem by yielding more
reliability ? How big an influence would noise
have upon misguided learning ? Wonder what
measures can prevent the local minimum traps.
15
Is there any mathematical validation for the
existence of a stopping point in validation
samples ? The number of hidden nodes are adjusted
by a human. An NN is supposed to self-learn and
therefore there must be a way to automatically
adjust the number of the hidden nodes.
16
(No Transcript)
17
? Normalize Inputs, Scale Outputs. Zero
mean, Decorrelate (PCA) and Covariance
equalization
18
? Start with small uniform random initial
weights for tanh
? Present training patterns in random (shuffled)
order (or mix different classes). ? Alternative
Cost or Activation Functions Ex.
Cost Use
with as
targets or (
, ,
at )
19
? Chen Mars Differential step size
Cf. Principes Book recommends
. Best to try diff. values.
? (Accelerating BP Algorithm through Omitting
Redundant Learning, J. of KIEE 92/9 ) If
, Ep lt ? do not update weight on the pth
training pattern NO BP
E
p
e
p
20
? Ahalt - Modular Net
? Ahalt - Adapt Slope (Sharpness) Parameters
vary ? in
21
? Jacobs - Learning Rate Adaptation
Ref. Neural Networks, Vol. 1, No. 4, 88.
a. Momentum
In plateau, where
is the effective learning rate
22
b. rule
where
For actual parameters to be used, consult Jacobs
paper and also Getting a fast break with
Backprop, Tveter, AI Expert Magazine, excerpt
from pdf files that I provided.
23
Students Questions from 2005 Is there any way to
design a spherical error surface for faster
convergence ? Momentum provides inertia to jump
over a small peak. Parameter Optimization
technique seems to a good help to NN design. I am
afraid that optimizing even the sigmoid slope and
the learning rate may expedite overfitting. In
what aspect is it more manageable to remove the
mean, decorrelate, etc. ? How does using a bigger
learning rate for the output layer help learning
? Does the solution always converge if we use the
gradient descent ?
24
Are there any shortcomings in using fast learning
algorithms ? In the Ahalts modular net, is it
faster for a single output only or all the
outputs than an MLP ? Various fast learning
methods have been proposed. Which is the best one
? Is it problem-dependent ? The Jacobs method
cannot find the global min. for an error surface
like
25
? Conjugate Gradient Fletcher Reeves
Line Search
If ? is fixed and
? Gradient Descent
If
? Steepest Descent
26
GradientDescent SteepestDescent
ConjugateGradient
Gradient D. Line Search Steepest
Descent Momentum
SD
GD
w(n)
w(n1)
w(n)
w(n1)
w(n2)
w(n2)
Momentum
CG
w(n)
w(n1)
w(n-1)
w(n)
s(n1)
w(n1)
27
If
Conjugate Gradient 1)
Line Search
2) Choose ? such that
From Polak-Ribiere Rule
28
START
Initialize
Line Search
N
Y
Y
N
29
Comparison of SD and CG
Steepest Descent
Conjugate Gradient
Each step takes a line search. For N-variable
quadratic functions, converges in N steps at
most Recommended Steepest Descent n
steps of Conjugate Gradient Steepest
Descent n steps of Conjugate Gradient
???
30
X. Swarm Intelligence
- What is swarm intelligence and why is it
- interesting?
- Two kinds of swarm intelligence
- particle swarm optimization
- ant colony optimization
- Some applications
- Discussion
31
What is Swarm intelligence?
- Swarm Intelligence is a property of systems of
non-intelligent agents exhibiting collectively
intelligent behavior. - Characteristics of a swarm
- distributed, no central control or data source
- no (explicit) model of the environment
- perception of environment
- ability to change environment
I cant do
We can do
32
Group of friends each having a metal detector are
on a treasure finding mission. Each can
communicate the signal and current position to
the n nearest neighbors. If you neighbor is
closer to the treasure than him, you can move
closer to that neighbor thereby improving your
own chance of finding the treasure. Also, the
treasure may be found more easily than if you
were on your own. Individuals in a swarm
interact to solve a global objective in a more
efficient manner than one single individual
could. A swarm is defined as a structured
collection of interacting organisms ants, bees,
wasps, termites, fish in schools an birds in
flocks or agents. Within the swarms,
individuals are simple in structure, but their
collective behaviors can be quite complex. Hence,
the global behavior of a swam emerges in a
nonlinear manner from the behavior of the
individuals in that swarm. The interaction among
individuals plays a vital role in shaping the
swarms behavior. Interaction aids in refining
experiential knowledge about the environment, and
enhances the progress of the swarm toward
optimality. The interaction is determined
genetically or throgh social interaction. Applicat
ions function optimization, optimal route
finding, scheduling, image and data analysis.
33
Why is it interesting?
- Robust nature of animal problem-solving
- simple creatures exhibit complex behavior
- behavior modified by dynamic environment
- e.g.) ants, bees, birds, fishes, etc,.
34
Two kinds of Swarm intelligence
- Particle swarm optimization
- Proposed in 1995 by J. Kennedy and R. C.
Eberhart - based on the behavior of bird flocks and fish
schools - Ant colony optimization
- defined in 1999 by Dorigo, Di Cargo and
Gambardella - based on the behavior of ant colonies
35
1. Particle Swarm Optimization
- Population-based method
- Has three main principles
- a particle has a movement
- this particle wants to go back to the best
previously visited position - this particle tries to get to the position of
the best positioned particles
36
- Four types of neighborhood
- star (global) all particles are neighbors of
all - particles
- ring (circle) particles have a fixed number of
- neighbors K (usually 2)
- wheel only one particle is connected to all
- particles and act as hub
- random N random conections are made between
- the particles
37
(No Transcript)
38
- algorithm
Initialization
xid(0) random value, vid(0) 0
Calculate performance
F (xid(t)) ? (F performance)
Update best particle
F (xid(t)) is better than the pbest -gt pbest
F(xid(t)), pid xid(t), Same for the gbest
Move each particle
See next slide
Until system converges
39
- Particle Dynamics
for convergence c1 c2 lt 4 Kennedy 1998
40
(No Transcript)
41
(No Transcript)
42
- Examples
http//uk.geocities.com/markcsinclair/pso.html
http//www.engr.iupui.edu/shi/PSO/AppletGUI.html
43
? Fuzzy control of Learning rate, Slope
(Principes, Chap. 4.16)
? Local Minimum Problem
- Restart with different initial weights, learning
rates, and number - of hidden nodes
- Add (and anneal) noise a little (zero mean white
Gaussian) to
weights or training data desired output or input
(for better generalization) - Use Simulated Annealing or Genetic Algorithm
Optimization then BP
? Design aided by a Graphic User Interface NN
Oscilloscope
Look at Internal weights/Node Activities with
Color Coding
44
Students Questions from 2005 When the learning
rate is optimized and initialized, there must be
a rough boundary for it. Just an empirical way to
do it ? In Conjugate Gradient, s(n) -g(n1)
The learning rate annealing just keeps on
decreasing the error as n without looking at
where in the error surface the current weights
are. Is this OK ? Conjugate Gradient is similar
to Momentum in that old search direction is
utilized in determining the new search direction.
It is also similar to rule using the past
trend. Is CG always faster converging than the SD
? Do the diff. initial values of the weights
affect the output results ? How can we choose
them ?