Crystal Structure - PowerPoint PPT Presentation
Title:
Crystal Structure
Description:
Crystal Structure Examples of Crystals Examples of Crystals Tightest Way to Pack Spheres (II) ABC stacking Sequence (FCC) ABAB stacking Sequence (HCP) Cubic ... – PowerPoint PPT presentation
Number of Views:1197
Avg rating:3.0/5.0
Title: Crystal Structure
1
Crystal Structure
2
Crystal Properties of Semiconductors
3
(No Transcript)
4
d
f
i
c
a
t
i
o
n
o
f
a
p
o
l
y
c
r
y
s
t
a
l
l
i
n
e
s
o
l
i
d
f
r
o
m
t
h
e
m
e
l
t
.
(
a
)
N
u
c
l
e
a
t
i
o
n
.
(
b
)
r
o
w
h
.
(
c
)
T
h
e
s
o
l
i
d
i
f
i
e
d
p
o
l
y
c
r
y
s
t
a
l
l
i
n
e
s
o
l
i
d
.
F
o
r
S
c
s
i
m
p
l
i
i
t
y
,
c
u
b
e
s
r
e
p
r
e
s
e
n
t
a
t
o
m
s
.
5
Crystal Properties of Solid
- Polycrystalline
G
r
a
i
n
1
G
r
a
i
n
2
G
r
a
i
n
B
o
u
n
d
a
r
y
(a)
(
b
)
G
r
a
i
n
b
o
u
n
d
a
r
i
e
s
c
a
u
s
e
s
c
a
t
t
e
r
i
n
g
o
f
t
h
e
e
l
e
c
t
r
o
n
a
n
d
t
h
e
r
e
f
o
i
a
m
e
t
e
r
.
6
Crystal Properties of Solid
- Polycrystalline
F
o
r
e
i
g
n
i
m
p
u
r
i
t
y
S
e
l
f
-
i
n
t
e
r
s
t
i
t
i
a
l
t
y
p
e
a
t
o
m
V
o
i
d
,
v
a
c
a
n
c
y
b
o
n
d
G
r
a
i
n
b
o
u
n
d
a
r
y
B
r
o
k
e
n
b
o
n
d
(
d
a
n
g
l
i
n
g
b
o
n
d
)
T
h
e
g
r
a
i
n
b
o
u
n
d
a
r
i
e
s
h
a
v
e
b
r
o
k
e
n
b
o
n
d
s
,
v
o
i
d
s
,
v
a
c
a
n
c
i
e
s
,
s
t
r
a
i
n
e
d
b
o
n
d
s
a
n
d
"
i
n
t
e
r
s
t
i
t
i
a
l
"
t
y
p
e
a
t
o
m
s
.
T
h
e
s
t
r
u
c
t
u
r
e
o
f
t
h
e
g
r
a
i
n
b
o
u
n
d
a
r
y
i
s
d
i
s
o
r
d
e
r
e
d
a
n
d
t
h
e
a
t
o
m
s
i
n
t
h
e
g
r
a
i
n
b
o
u
n
d
a
r
i
e
s
h
a
v
e
h
i
g
h
e
r
e
n
e
r
g
i
e
s
t
h
a
n
t
h
o
s
e
w
i
t
h
i
n
t
h
e
g
r
a
i
n
s
.
7
Examples of Crystals
Snow
Quartz
Copper oxide
Salt (NaCl) crystal
Gold (Au) crystals at 1000 C
8
Examples of Crystals
Salt (NaCl) crystal
9
Examples of Crystals
Carbon Nanotube
Carbon Nanofiber
Fullerene
TEM image of Carbon Nanotube
10
Examples of Crystals
Single crystal Diamonds.
Single crystal Silicon.
11
Atomic Resolution Images of Solid Surfaces
- STM (Scanning Tunneling Microscope) images of
solid surface
Silicon (Si) surface
Iron silicide surface
12
Atomic Resolution Images of Solid Surfaces
- 3D-STM (Scanning Tunneling Microscope) images
of solid surface
Silicon (Si) surface
Hydrogen bonds on a Silicon surface.
13
Atomic Resolution Images of Solid Surfaces
- TEM (Tunneling Electron Microscope) images of
solid surface
High resolution image of a quasiperiodical grain
boundary in gold.
14
Crystal Structures and Definitions
- Lattice The periodic arrangement of the atoms.
- Unit Cell
- Representative of the entire lattice and is
regularly repeated throughout the crystal. - Primitive Cell
- Smallest unit cell which can be repeated to
form the lattices.
a
a/2
Primitive Cell
Unit Cell
Each crystal built up of a repetitive stacking of
unit cells each identical in size,
shape, and orientation with every other one.
15
Crystal Structures and Definitions
- Coordinates of position in the unit cell
- x, y, z expressed in terms of the unit cell
edges. - Example
- reached by moving along the axis a distance
of - 3x the length of the vector , the
parallel to , a distance 2? , - and finally parallel to , a
distance equal to the length of .
16
Crystal Lattice Group
- Bravais lattices
Length and Angle
Triclinic a?b?c ??????90? K2CrO7 Monoclinic a?
b?c ??90??? ?-S, CaSO4?2H2O Orthorhombic
a?b?c ???90? ?-S, Ga,
Fe3C Tetragonal ab?c ???90? ?-Sn,
TiO2 Cubic abc ???90? Cu, Ag, Zn,
NaCl Hexagonal a1a2a3?c ??90?, ?120?
Zn, Cd Rhombohedral abc ????90? As,
Sb, Bi
17
Crystal (Bravais) Lattice Group (I)
Monoclinic a?b?c, ??90 ??90 Monoclinic a?b?c, ??90 ??90
Orthorhombica?b?c, ???90 Orthorhombic a?b?c, ???90 Orthorhombic a?b?c, ???90
Triclinic a?b?c, ??????90
18
Crystal (Bravais) Lattice Group (II)
Orthorhombic a?b?c, ???90 Hexagonal a1a2a3?c, ??90 ?120 Rhombohedral abc, ????90
19
Crystal (Bravais) Lattice Group (III)
Tetragonal ab?c, ???90 Tetragonal ab?c, ???90 Cubicabc, ???90
Cubic abc, ???90 Cubic abc, ???90
20
U
N
I
T
C
E
L
L
G
E
O
M
E
T
R
Y
C
U
B
I
C
S
Y
S
T
E
M
a
b
g
a
b
c
9
0
M
a
H
e
x
a
g
o
n
a
l
m
b
o
h
e
d
r
a
l
F
l
u
o
r
i
d
e
B
a
s
e
c
e
n
t
e
r
e
d
T
r
i
c
l
i
n
i
c
m
o
n
o
c
l
i
n
i
c
21
Miller Convention Summary
Convention Interpretation (hkl) Crystal
Plane hkl Equivalent Planes
hkl Crystal Direction lthklgt Equivalent
Directions
- Examples
? plane 111 (111) (-111) (1-11) (11-1)
? direction lt111gt 111 -111 1-11 11-1
22
Crystal Planes
- Identification of a plan in a crystal
z
z
i
n
t
e
r
c
e
p
t
a
t
b
Miller Indices (hkl)
1
1
1
(
210)
1
1
c
/
2
a
x
/
i
n
t
e
r
c
e
p
t
a
t
2
y
a
y
b
i
n
t
e
r
c
e
p
t
a
t
U
n
i
t
c
e
l
l
x
23
Crystal Planes
- Identification of a plane and direction in a
crystal
z
121
z
P
o
c
x
y
y
o
o
a
b
24
Crystal Planes
- Miller Index
25
Miller Index
- Examples
26
Miller Index
- Examples
27
Crystal Planes in the Cubic Lattice
- Various planes in cubic lattice
y
28
Crystal Planes
- Interplanar spacing
- The value of d, the distance between
adjacent planes in the set - (hkl), may be found from the following
equations - Cubic
- Tetragonal
?
29
Crystal Planes
- X-Ray Diffraction
- Each set of planes has a specific interplanar
distance and will give rise to a characteristic
angle of diffracted X-rays. - The relationship between wavelength, atomic
spacing (d) and angle was solved as the Bragg
Equation.
30
Crystal Planes
- Interplanar Angles
- Single ? between (h1 k1 l1) of sparing d,
and the plane (h2 k2 l2), of - spacing, may be found from the
followings. - Cubic cos?
- Tetragonal cos?
- Hexagonal cos?
?
31
Crystal Directions
- Crystal Directions in Cubic Crystal System
32
Cubic Lattices
- SC (Simple Cubic)
- Atoms situated at the corners of the unit cell.
- Atoms touch along lt100gt and a 2r (r atomic
radius) - BCC (Body-Centred Cubic)
- Atoms situated at the corners of the unit cell
and at the centre. - Atoms touch along lt111gt and a 4r/?3
- FCC (Face-Centred Cubic)
- Atoms situated at the corners of the unit cell
and at the centre of - all cubic faces.
- Atoms touch along lt110gt and a 2r/?2
?
33
Tightest Way to Pack Spheres (I)
ABC stacking Sequence (FCC)
ABAB stacking Sequence (HCP)
other close packed structures, ABABCAB etc.
34
Tightest Way to Pack Spheres (II)
ABC stacking Sequence (FCC)
ABAB stacking Sequence (HCP)
35
Cubic Structures
- Cubic Lattices
- Atoms situated at the corners of the unit cell.
a lattice constant
(a) Simple Cubic
(b) Body-Centered Cubic BCC
(C) Face-Centered Cubic FCC
36
Crystal Structure Model
- Characteristics of Cubic Lattices
-
Simple BCC FCC - Volume of cubic cell a3 a3 a3
- Volume of primitive cell a3 1/2a3 1/4a3
- Type of primitive cell SC rhombohedral
rhombohedral - Lattice points per cubic cell
1 2 4 - Lattice points per unit cell
1/a3 2/a3 4/a3 - Nearest neighbour distance a 1/2?3a 1/2?2a
- of nearest neighbours 6 8 12
- Next nearest neighbour distance ?2 a a a
- of next nearest neighbours 12 6
6
37
Crystal Structure Model
- Hard Sphere Model
- Assume that the atoms are considered as hard
spheres
- Simple CubicSC
(b) Body-Centered Cubic BCC
(C) Face Centered Cubic FCC
38
Crystal Structure Model
- FCC Lattices
(
a
)
T
h
e
c
r
y
s
t
a
l
s
t
r
u
c
t
u
r
e
o
f
c
o
p
p
e
r
i
s
F
a
c
e
C
e
n
t
e
r
e
d
C
u
b
i
c
(
F
C
C
)
.
T
h
e
a
t
o
m
s
a
r
e
p
o
s
i
t
i
o
n
e
d
a
t
w
e
l
l
d
e
f
i
n
e
d
s
i
t
e
s
a
r
r
a
n
g
e
d
p
e
r
i
o
d
i
c
a
l
l
y
a
n
d
t
h
e
r
e
i
s
a
l
o
n
g
r
a
n
g
e
o
r
d
e
r
i
n
t
h
e
c
r
y
s
t
a
l
.
(
b
)
A
n
F
C
C
u
n
i
t
c
e
l
l
w
i
t
h
c
l
o
s
e
d
p
a
c
k
e
d
s
p
h
e
r
e
s
.
(
c
)
R
e
d
u
c
e
d
s
p
h
e
r
e
r
e
p
r
e
s
e
n
t
a
t
i
o
n
o
f
t
h
e
F
C
C
u
n
i
t
g
c
e
l
l
.
E
x
a
m
p
l
e
s
A
g
,
A
l
,
A
u
,
C
a
,
C
u
,
-
F
e
(
gt
9
1
2
C
)
,
N
i
,
P
d
,
P
t
,
R
h
39
Crystal Structure Model
- BCC Lattices
a
(a)
(b)
E
x
a
m
p
l
e
s
A
l
k
a
l
i
m
e
t
a
l
s
(
L
i
,
N
a
,
K
,
R
b
)
,
C
r
,
a
b
M
o
,
W
,
M
n
,
-
F
e
(
lt
9
1
2
C
)
,
-
T
i
(
gt
8
8
2
C
)
.
B
o
d
y
c
e
n
t
e
r
e
d
c
u
b
i
c
(
B
C
C
)
c
r
y
s
t
a
l
s
t
r
u
c
t
u
r
e
.
(
a
)
u
n
i
t
c
e
l
l
w
i
t
h
c
l
o
s
e
l
y
p
a
c
k
e
d
h
a
r
d
s
p
h
e
r
e
s
r
e
p
r
e
s
e
n
t
i
n
g
t
h
e
F
e
a
t
o
m
s
.
(
b
)
A
r
e
d
u
c
e
d
-
s
p
h
e
r
e
u
n
i
t
c
e
l
l
.
40
Atomic Packing Factor
- Simple Cubic and FCC Lattices
Number of atoms
Volume of atoms
Number of atoms
Volume of atoms
Volume of unit cell
Volume of unit cell
41
Atomic Packing Factor
- Four Cubic Lattices
42
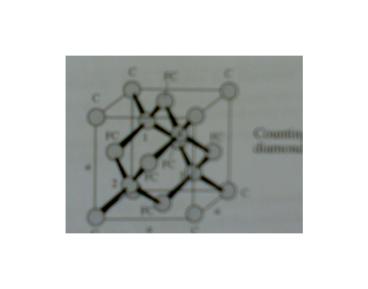
Semiconductor Lattice Structures
- Diamond Lattices
- The diamond-crystal lattice characterized by four
covalently bonded atoms. - The lattice constant, denoted by ao, is 0.356,
0.543 and 0.565 nm for diamond, silicon, and
germanium, respectively. - Nearest neighbors are spaced ( ) units
apart.
- Of the 18 atoms shown in the figure, only 8
belong to the volume ao3. Because the 8 corner
atoms are each shared by 8 cubes, they contribute
a total of 1 atom the 6 face atoms are each
shared by 2 cubes and thus contribute 3 atoms,
and there are 4 atoms inside the cube. The
atomic density is therefore 8/ao3, which
corresponds to 17.7, 5.00, and 4.43 X 1022 cm-3,
respectively.
(After W. Shockley Electrons and Holes in
Semiconductors, Van Nostrand, Princeton, N.J.,
1950.)
43
Semiconductor Lattice Structures
- Diamond Lattices
44
Semiconductor Lattice Structures
- Diamond and Zincblende Lattices
Diamond lattice can be though of as an FCC
structures with an extra atoms placed at
a/4b/4c/4 from each of the FCC atoms
Zincblende lattice GaAs, InP, ZnSe
Diamond lattice Si, Ge
The Zincblende lattice consist of a face centered
cubic Bravais point lattice which contains two
different atoms per lattice point. The distance
between the two atoms equals one quarter of the
body diagonal of the cube.
45
Semiconductor Lattice Structures
- Diamond and Zincblende Lattices
Diamond lattice Si, Ge
Zincblende lattice GaAs, InP, ZnSe
46
Crystal Surfaces and Atomic Arrangement
- Arrangement of atoms on various crystal
surfaces.
47
Low Miller Index Planes of Cubic Lattice
BCC
(111)
(100)
(110)
FCC
(111)
(100)
(110)
48
Low Miller Index Planes Diamond Lattice
- Diamond Lattice Structures
Number of atoms per unit cell 8 Atomic packing
factor 0.34 maximum packing density is 34 .
49
Crystal Directions and Atomic Arrangement
- Arrangement of atoms in Diamond lattice
structures -
on various crystal directions.
50
Actual Crystal Surfaces Observed by Scanning
Tunneling Microscope
Silicon (111) surface
Silicon (100) surface
51
Common Crystal Structures of Semiconductor
52
Semiconductor Materials
IV Compounds SiC, SiGe III-V Binary
Compounds AlP, AlAs, AlSb, GaN, GaP, GaAs,
GaSb, InP, InAs, InSb III-V Ternary
Compounds AlGaAs, InGaAs, AlGaP III-V Quternary
Compounds AlGaAsP, InGaAsP II-VI Binary
Compounds ZnS, ZnSe, ZnTe, CdS, CdSe,
CdTe II-VI Ternary Compounds HgCdTe
53
Semiconductor Materials