Graph the equation of a translated circle PowerPoint PPT Presentation
Title: Graph the equation of a translated circle
1
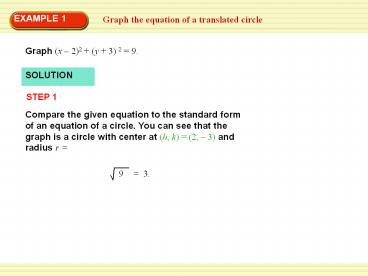
EXAMPLE 1
Graph the equation of a translated circle
Graph (x 2)2 (y 3) 2 9.
SOLUTION
STEP 1
2
EXAMPLE 1
Graph the equation of a translated circle
STEP 2
Plot the center. Then plot several points that
are each 3 units from the center
(2 3, 3) (5, 3)
(2 3, 3) ( 1, 3)
(2, 3 3) (2, 0)
(2, 3 3) (2, 6)
STEP 3
Draw a circle through the points.
3
EXAMPLE 2
Graph the equation of a translated hyperbola
Graph
1
SOLUTION
STEP 1
Compare the given equation to the standard forms
of equations of hyperbolas. The equations form
tells you that the graph is a hyperbola with a
vertical transverse axis. The center is at (h, k)
( 1, 3). Because a2 4 and b2 9, you know
that a 2 and b 3.
4
EXAMPLE 2
Graph the equation of a translated hyperbola
STEP 2
5
EXAMPLE 2
Graph the equation of a translated hyperbola
STEP 3
Draw the hyperbola. Draw a rectangle centered at
(21, 3) that is 2a 4 units high and 2b
6 units wide. Draw the asymptotes through the
opposite corners of the rectangle. Then draw the
hyperbola passing through the vertices and
approaching the asymptotes.
6
EXAMPLE 3
Write an equation of a translated parabola
Write an equation of the parabola whose vertex is
at ( 2, 3) and whose focus is at (
4, 3).
SOLUTION
STEP 1
Determine the form of the equation. Begin by
making a rough sketch of the parabola. Because
the focus is to the left of the vertex, the
parabola opens to the left, and its equation has
the form
(y k)2 4p(x h) where p lt 0.
7
EXAMPLE 3
Write an equation of a translated parabola
STEP 2
Identify h and k. The vertex is at ( 2,
3), so h 2 and k 3.
STEP 3
Find p. The vertex ( 2, 3) and focus (?4, 3)
both lie on the line y 3, so the distance
between them is p
4 ( 2) 2, and thus p 2. Because p lt
0, it follows that p 2, so 4p 8.
8
EXAMPLE 3
Write an equation of a translated parabola
ANSWER
The standard form of the equation is
(y 3)2 8(x
2).
9
EXAMPLE 4
Write an equation of a translated ellipse
Write an equation of the ellipse with foci at (1,
2) and (7, 2) and co-vertices at (4,
0) and (4, 4).
SOLUTION
STEP 1
Determine the form of the equation. First sketch
the ellipse. The foci lie on the major axis, so
the axis is horizontal. The equation has this
form
10
EXAMPLE 4
Write an equation of a translated ellipse
STEP 2
Identify h and k by finding the center, which is
halfway between the foci (or the co-vertices)
(4, 2)
STEP 3
Find b, the distance between a co-vertex and the
center (4, 2), and c, the distance between a
focus and the center. Choose the co-vertex (4, 4)
and the focus (1, 2) b 4 2 2 and c
1 4 3.
11
EXAMPLE 4
Write an equation of a translated ellipse
STEP 4
12
EXAMPLE 5
Identify symmetries of conic sections
Identify the line(s) of symmetry for each conic
section in Examples 1 4.
SOLUTION
For the hyperbola in Example 2 x 1 and y 3
are lines of symmetry
For the circle in Example 1, any line through the
center (2, 3) is a line of symmetry.
13
EXAMPLE 5
Identify symmetries of conic sections
For the ellipse in Example 4, x
4 and y 2 are lines of symmetry.
For the parabola in Example 3, y 3 is a line of
symmetry.
14
EXAMPLE 6
Classify a conic
Classify the conic given by 4x2 y2 8x 8
0. Then graph the equation.
SOLUTION
4x2 y2 8x 8 0
(4x2 8x) y2 8
4(x2 2x) y2 8
4(x2 2x ? ) y2 8 4( ? )
15
EXAMPLE 6
Classify a conic
4(x2 2x 1) y2 8 4(1)
4(x 1)2 y2 12
16
EXAMPLE 1
Solve a linear-quadratic system by graphing
Solve the system using a graphing calculator.
y2 7x 3 0
Equation 1
2x y 3
Equation 2
SOLUTION
y2 7x 3 0
2x y 3
y2 7x 3
y 2x 3
y 2x 3
Equation 1
Equation 2
17
EXAMPLE 1
Solve a linear-quadratic system by graphing
18
EXAMPLE 1
Solve a linear-quadratic system by graphing
19
EXAMPLE 2
Solve a linear-quadratic system by substitution
Solve the system using substitution.
x2 y2 10
Equation 1
y 3x 10
Equation 2
SOLUTION
Substitute 3x 10 for y in Equation 1 and solve
for x.
Equation 1
x2 y2 10
x2 ( 3x 10)2 10
Substitute for y.
x2 9x2 60x 100 10
Expand the power.
10x2 60x 90 0
Combine like terms.
x2 6x 9 0
Divide each side by 10.
(x 3)2 0
Perfect square trinomial
x 3
Zero product property
20
EXAMPLE 2
Solve a linear-quadratic system by substitution
y 3(3) 10 1
CHECK You can check the solution by graphing the
equations in the system. You can see from the
graph shown that the line and the circle
intersect only at the point (3, 1).
21
EXAMPLE 3
Solve a quadratic system by elimination
Solve the system by elimination.
9x2 y2 90x 216 0
Equation 1
x2 y2 16 0
Equation 2
SOLUTION
9x2 y2 90x 216 0
10x2 90x 200 0
Add.
x2 9x 20 0
Divide each side by 10.
(x 4)(x 5) 0
Factor
x 4 or x 5
Zero product property
22
EXAMPLE 3
Solve a quadratic system by elimination
When x 4, y 0. When x 5, y 3.
23
EXAMPLE 4
Solve a real-life quadratic system
Navigation
24
EXAMPLE 4
Solve a real-life quadratic system
x2 y2 16x 32 0
Equation 1
x2 y2 8y 8 0
Equation 2
SOLUTION
x2 y2 16x 32 0
16x 8y 40 0
Add.
y 2x 5
Solve for y.
25
EXAMPLE 4
Solve a real-life quadratic system
x2 y2 16x 32 0
Equation 1
x2 (?2x 5)2 16x 32 0
Substitute for y.
3x2 4x 7 0
Simplify.
(x 1)(3x 7) 0
Factor.
Zero product property
26
EXAMPLE 4
Solve a real-life quadratic system