Chapter 2 Preliminary calculus

1
Chapter 2 Preliminary calculus
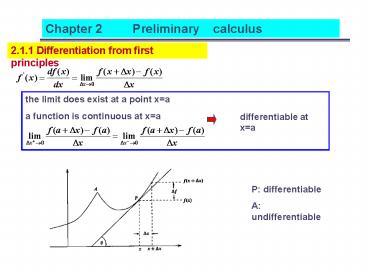
2.1.1 Differentiation from first principles
the limit does exist at a point xa a function
is continuous at xa
differentiable at xa
P differentiable A undifferentiable
2
Chapter 2 Preliminary calculus
high order derivative
useful formulas
Hint
3
Chapter 2 Preliminary calculus
2.1.2 Differentiation of products
2.1.2 Differentiation of product

2.1.3 The chain rule
2.1.4 Differentiation of quotients
2.1.5 Implicit differentiation
4
Chapter 2 Preliminary calculus
2.1.6 Logarithmic differentiation
2.1.7 Leibnitz theorem
5
Chapter 2 Preliminary calculus
Ex Find the third derivative of the function
,and set
2.1.8 Special points of a function
Q
(1) local maximum Q (2) local minimum B (3)
stationary point of inflection S
stationary points
S
B
6
Chapter 2 Preliminary calculus
(1) for a local minimum
(2) for a local maximum
(3) for a stationary point of inflection
and
changes sign through the point, so
Ex
(1) for
is a minimum
(2) for
is a maximum
7
Chapter 2 Preliminary calculus

• general points of inflection

(1)
changes sign from the left (concave upwards) to
the right (concave downwards).
(2)

• note a stationary point of inflection with
• is a special case

8
Chapter 2 Preliminary calculus
2.1.9 Curvature of a function
(1) at point P
(2)
the radius of curvature
the curvature of
at P
the curve is locally concave upwards
the curve is locally concave downwards
9
Chapter 2 Preliminary calculus

• the radius of curvature in terms of x and f(x)

ds
?
dx

• for a stationary point of inflection
• and the curvature is zero

10
Chapter 2 Preliminary calculus
Ex Show that the radius of curvature at the
point (x,y) on the ellipse
and the opposite
has magnitude
sign to y. Check the special case ba, for which
the ellipse becomes a circle.
Sol
differentiating the equation
determines the sign of
for ba
the function is a circle.
11
Chapter 2 Preliminary calculus
2.1.9 Theorem of differentation

• Rolles theorem

(1) f(x) is continuous for
(2) f(x) is differentiable for
at least one point
Proof
f(x)
(1) if
is a constant
(2)
x
if
a b c
12
Chapter 2 Preliminary calculus

• Mean value theorem

(1) f(x) is continuous for
and
(2) f(x) is differentiable for
at least one value b ( a lt b lt c) such that
f(x) f(c)
Proof
the equation of the line AC is
C
A
f(a)
g(x)
by Rolles theorem, at least one
x
a b c
point
13
Chapter 2 Preliminary calculus
Ex What semi-quantitative results can be deduced
by Rolles theorem to the following function,
with a and c are chosen so that f(a)f(c)0?

Sol
(i)
(ii)
(iii)
(v)
are two different roots if

or

are three different roots if
14
Chapter 2 Preliminary calculus
2.2 Integration
f(x)

• integration from principles

x
a b

• integration as the inverse of differentiation

a is arbitrary
15
Chapter 2 Preliminary calculus

• definite integral

• integration by inspection

(1)
Sol
(2)
(3)
Hint
set and
16
Chapter 2 Preliminary calculus
(4)
(5)
(6)
Hint

• integration of sinusoidal function

(1)
(2)
17
Chapter 2 Preliminary calculus

• logarithmic integration

Ex

• integration using partial fractions

Ex

• integration by substitution

Hint set
Ex
18
Chapter 2 Preliminary calculus
Ex
set
Ex
set
19
Chapter 2 Preliminary calculus

• integration by parts

Ex
set
Ex
set
20
Chapter 2 Preliminary calculus
Ex
set
21
Chapter 2 Preliminary calculus

• reduction formula

Ex
to evaluate
set
22
Chapter 2 Preliminary calculus

• infinite integrals

Ex

• improper integrals

Ex
23
Chapter 2 Preliminary calculus

• integration in plane polar coordinates

C
y
the area of a circle is
dA
Ex
Find the area of an ellipse with an equation
B
0
x
set
24
Chapter 2 Preliminary calculus

• finding the length of a curve

f(x)
yf(x)
x
in plane polar coordinate
25
Chapter 2 Preliminary calculus
surface area
Ex
Find the surface area of a cone formed by
rotating about the x-axis the line y2x between
x0 and xh.
Sol

• if the surface is formed by rotating a line
  about the y-axis

26
Chapter 2 Preliminary calculus

• volumes of revolution

Ex
Find the volume of a cone enclosed by the surface
formed by rotating about the x-axis the line y2x
between x0 and xh.
Sol