Desired Bode plot shape

1
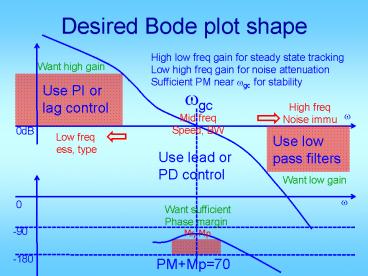
Desired Bode plot shape
High low freq gain for steady state tracking Low
high freq gain for noise attenuation Sufficient
PM near wgc for stability
Want high gain
Use PI or lag control
wgc
High freq Noise immu
w
Mid freq Speed, BW
0dB
Low freq ess, type
Use low pass filters
Use lead or PD control
Want low gain
w
0
Want sufficient Phase margin
-90
Mr, Mp
-180
PMMp70
2
Overall Loop shaping strategy

• Determine mid freq requirements
• Speed/bandwidth ? wgc
• Overshoot/resonance ? PMd
• Use PD or lead to achieve PMd_at_ wgc
• Use overall gain K to enforce wgc
• PI or lag to improve steady state tracking
• Use PI if type increase neede
• Use lag if ess needs to be reduced
• Use low pass filter to reduce high freq gain

3
Proportional controller design

• Obtain open loop Bode plot
• Convert design specs into Bode plot req.
• Select KP based on requirements
• For improving ess KP Kp,v,a,des / Kp,v,a,act
• For fixing Mp select wgcd to be the freq at
  which PM is sufficient, and KP 1/G(jwgcd)
• For fixing speed from td, tr, tp, or ts
  requirement, find out wn, let wgcd
  (0.650.8)wn and KP 1/G(jwgcd)

4
PD control design
5
PD control design Variation

• Restricted to using KP 1
• Meet Mp requirement
• Find wgc and PM
• Find PMd
• Let f PMd PM (a few degrees)
• Compute TD tan(f)/wgcd
• KP 1 KDKPTD

6
Lead Design

• From specs gt PMd and wgcd
• From plant, draw Bode plot
• Find PMhave 180 angle(G(jwgcd)
• DPM PMd - PMhave a few degrees
• Choose aplead/zlead so that fmax DPM and it
  happens at wgcd

7
Alternative use of lead

1. Select K so that KG(s) meet ess req.
2. Find wgc and PM, also find PMd
3. Determine phi_max, and alpha
4. Place phi_max a little higher than wgc

8
Lag Controller Design
9
Lag and lead-lag Design Steps

• From plant, draw Bode plot
• From specs gt PMd and wgcd
• If there is speed or BW req, ? wgcd,
• In this case, if PM not enough, design PD or lead
• Otherwise, choose wgcd to have PMgtPMd
• Find K to enforce wgcd
• Find Kp,v,a-have with K and C above
• Find Kp,v,a-des from ess specs
• zlag/plag Kp,v,a-des/Kp,v,a-have
• Let zlag wgcd/520, depending on PM room
• Compute plag

10
PI Controller
11
PI Controller Design
Use PI only when you have to increase system
type, i.e., when you have to make a nonzero ess
to zero!
12
Gain/Kp In dB
Type ? LF gain ? ess ?
wz
Let wgc/z big
Big phase ? Detabilizing
w/z
13
PI controller design

• Choice 1 first multiply G by 1/s, then do PD
• Choice 2 KPKI/sKP (sz)/s
• Do proportional controller design for wgc, PM
• ? Kp
• Place zero of PI controller at 10 to 20 times
  smaller than wgc
• ? zwgc/(1020)
• KIKKP z

14
KI/KPwgcd/2
KI/KPwgcd/5
KI/KPwgcd/10
Want these DC gain boosting
KI/KPwgcd/20
wgcd
KI/KPwgcd/40
-5.7
-2.8
-1.4
-11.3
-26. 6
Kill PM significantly
Dont want these PM reduction!
15
Basic PI Design Steps

• From plant, draw Bode plot
• From specs gt PMd and wgcd
• If there is speed or BW req, ? wgcd,
• In this case, if PM not enough, design PD or lead
• Otherwise, choose wgcd to have PMgtPMd
• Find K to enforce wgcd
• Let KP K
• And KI Kwgcd/1020, depending on extra PM room
  to spare

Need to increase type to make a nonzero ess to be
zero. But no requirement on ess after type
increase.
16
Example
Want Mp lt 16 Steady state error 0 when input
is constant.
Analysis steady state error 0 when input is
constant means that ess to step must be 0 or the
system type must be 1 or higher. Original system
is type 0, so need PI control to increase the
system type to 1.
17
PI control example n500 d1 6
5 figure(1) clf margin(n,d) hold on grid
Vaxis Mp 16 PMd 70 - Mp 10 put in a
large extra PM, because PI kills
PM semilogx(V(12),PMd-180 PMd-180,'r') draw
PMd line xginput(1) w_gcd x(1) get desired
w_gc KP 1/abs(polyval(n,jw_gcd)/polyval(d,jw_g
cd)) z w_gcd/10 KI zKP ngc conv(n, KP
KI) dgc conv(d, 1 0) figure(1)
margin(ngc,dgc) grid ncl,dclfeedback(ngc,dgc
,1,1) figure(2)step(ncl,dcl) grid figure(3)
margin(ncl1.414,dcl) grid
18
(No Transcript)
19
(No Transcript)
20
Ess is 0
Can afford more overshoot!
21
Sluggish settling is typical of PI or lag
controlled systems. Can reduce it by moving the
p and z of lag or PI controller to higher
frequency.
22
(No Transcript)
23
PI control example n500 d1 6
5 figure(1) clf margin(n,d) hold on grid
Vaxis Mp 16 PMd 70 - Mp 10 put in a
large extra PM, because PI kills
PM semilogx(V(12),PMd-180 PMd-180,'r') draw
PMd line xginput(1) w_gcd x(1) get desired
w_gc KP 1/abs(polyval(n,jw_gcd)/polyval(d,jw_g
cd)) z w_gcd/5 KI zKP ngc conv(n, KP
KI) dgc conv(d, 1 0) figure(1)
margin(ngc,dgc) grid ncl,dclfeedback(ngc,dgc
,1,1) figure(2)step(ncl,dcl) grid figure(3)
margin(ncl1.414,dcl) grid
24
(No Transcript)
25
(No Transcript)
26
PI Design with ess specs

• From plant, draw Bode plot
• From specs gt Kv,a-des, PMd and wgcd
• For required ess, Kv,a-des 1/ess
• With C(s)1/s, compute Kv,a-have
• If there is speed or BW req, ? wgcd,
• In this case, if PM not enough, design PD or lead
• Otherwise, choose wgcd to have PMgtPMd
• Find K to enforce wgcd
• Let KP K, KIdes Kv,a-des/Kv,a-have
• If KIdes lt Kwgcd/520, done, let KI KIdes
• Else, increase wgcd and go back to previous step

Need to increase type by 1 to make a nonzero ess
to be zero, and after type increase, there is
further requirement on ess.
27
Example
Want Mp lt 16 Steady state error lt 0.1 for ramp
input.
Analysis steady state error lt 0.1 for ramp
implies that the system type must be 1 or
higher. Original system is type 0, so need PI
control. Ess to ramp lt 0.1 requires Kvd gt
10. Previous design leaves Kv KI500/5 100KI
4.44
KI0.0444
28
This is actually the ramp response, generated
with the step command but the closed-loop TF is
multiplied by 1/s.
29
essgt0.1
30
In the previous design, KI0.0444 is already at
the maximum of the range Kwgcd/520, But KIdes
0.1, which is a factor of 10/4.44 larger. So
need to increase KP. Hence, try letting KI
KIdes 0.1, and make KP larger by 10/4.44.
31
Old KI, new KI
KP KP0.1/KI KI 0.1 ngc conv(n, KP
KI) dgc conv(d, 1 0) figure(1)
margin(ngc,dgc) grid ncl,dclfeedback(ngc,dgc,
1,1) figure(2)step(ncl,dcl) grid figure(3)
step(ncl,dcl 0) grid
Ramp response
32
(No Transcript)
33
ess 0.1
34
Can play with KP, but difficult to achieve the
best KP
35
PI Design with PD Design Steps

• From required ess, Kv,a-des 1/ess
• With C(s)1/s, compute Kv,a-have
• Let KI Kv,a-des/Kv,a-have
• Multiply G(s) by KI/s
• Do a PD design for KIG(s)/s, with DC gain1
• Find wgc and PM
• Find PMd
• Let f PMd PM (a few degrees)
• Compute TD tan(f)/wgcd
• KP KITD

36
Alternative PI control by PD design clear all
n0 0 500 d1 6 5 ess2ramp 0.1 Kvd
1/ess2ramp Kva n(end)/d(end) after
introducing 1/s KI Kvd/Kva multiplying G(s)
by KI/s and get new Bode niKIn did
0 figure(1) clf margin(ni,di) hold on
grid GM,PM,wpc,wgcmargin(ni,di) PMd546
phi (PMd-PM)pi/180 Td tan(phi)/wgc
KPKITd ngc conv(n, KP KI)
dgcdi figure(1) margin(n,d)
margin(ngc,dgc) ncl,dclfeedback(ngc,dgc,1,1)
figure(3)step(ncl,dcl) grid
37
(No Transcript)
38
(No Transcript)
39
clear all n0 0 500 d1 6 5 ess2ramp
0.1 Kvd 1/ess2ramp Kva n(end)/d(end)
after introducing 1/s KI Kvd/Kva multiplying
G(s) by KI/s and get new Bode niKIn did
0 figure(1) clf margin(ni,di) hold on
grid GM,PM,wpc,wgcmargin(ni,di) PMd503
phi (PMd-PM)pi/180 Td tan(phi)/wgc
KPKITd ngc conv(n, KP KI)
dgcdi figure(1) margin(n,d)
margin(ngc,dgc) ncl,dclfeedback(ngc,dgc,1,1)
figure(3)step(ncl,dcl) grid
40
(No Transcript)
41
(No Transcript)
42
Alternative PI Design Steps

• For required ess, Kv,a-des 1/ess
• With C(s)1/s, compute Kv,a-have
• Let KI Kv,a-des/Kv,a-have
• Rewrite char eq (KP KI/s)G(s) 10
• KPn/d KIn/d/s 1 0
• KP ns KInds 0, KPns/(KInds) 1 0
• So do a KP design for ns/(KInds), with KI
  above
• Draw Bode plot for ns/(KInds)
• Select max PM frequency
• Compute KP to make that frequency wgc

43
Alternative PI control example clear all n0 0
500 d1 6 5 note same length ess2ramp
0.1 Kvd 1/ess2ramp Kva n(end)/d(end)
after introducing 1/s KI Kvd/Kva get TF
after closing the G(s) and KI/s loop nin 0
did 0KI0 n figure(1) clf margin(ni,di)
grid xginput(1) w_gcd x(1) get desired
w_gc KP 1/abs(polyval(ni,jw_gcd)/polyval(di,jw
_gcd)) ngc conv(n, KP KI) dgc conv(d, 1
0) figure(2) margin(n,d) hold on
margin(ngc,dgc) ncl,dclfeedback(ngc,dgc,1,1)
figure(3)step(ncl,dcl) grid
44
Pick wgc here
45
(No Transcript)
46
(No Transcript)
47
Pick wgc here
48
(No Transcript)
49
(No Transcript)
50
Pick wgc here
51
(No Transcript)
52
Numerical sweep of KP indicates that 30 Mp is
about the best one can achieve. We conclude that
it is impossible to meet the specifications with
a PI controller. Both of our design procedures
came very close to the best achievable. Of
course, we can fix the excessive overshoot with
an additional lead design.
53
Want Mp lt 16 Steady state error lt 0.1 for ramp
input.

• Overall design
• Ess2ramp lt0.1, ? PI with KI1/0.15/5000.1
• Close the I-loop and select KP for best PM shape,
  ? KP 0.084
• Use a lead controller with DC gain 1 to reduce
  Mp from 30 to lt 16

54
clear all n0 0 500 d1 6 5 ess2ramp
0.1 Kvd 1/ess2ramp Kva n(end)/d(end)
after introducing 1/s KI Kvd/Kva get TF
after closing the G(s) and KI/s loop nin 0
did 0KI0 n figure(1) clf margin(ni,di)
grid xginput(1) w_gcd x(1) get desired
w_gc KP 1/abs(polyval(ni,jw_gcd)/polyval(di,jw
_gcd)) ngc conv(n, KP KI) dgc conv(d, 1
0) figure(2) margin(n,d) hold on
margin(ngc,dgc) ncl,dclfeedback(ngc,dgc,1,1)
figure(3)step(ncl,dcl) grid
55
follow with a lead controller with DC gain 1
to make Mp30 gt Mplt16 GM,PM,wpc,wgcmargi
n(ngc,dgc) w_gcdwgc PMd546 phimax
(PMd-PM)pi/180 alpha(1sin(phimax))/(1-sin(phim
ax)) zleadw_gcd/alpha.25 pleadw_gcdalpha.75
ngcc conv(ngc, alpha1 zlead) dgcc
conv(dgc, 1 plead) figure(2)
margin(ngcc,dgcc) grid ncl,dclfeedback(ngcc,d
gcc,1,1) figure(5)step(ncl,dcl)
grid figure(6)step(ncl,dcl 0) grid ramp
response
56
Original system
After PI alone
With PI and lead
57
Mp lt 16 is met.
58
(No Transcript)
59
yt
Ess0.1