Quiz Answers - PowerPoint PPT Presentation
1 / 54
Title:
Quiz Answers
Description:
Title: Superelevation and Spiral Curves Author: elatella Last modified by: CTRE Created Date: 2/15/2002 7:37:35 PM Document presentation format: On-screen Show – PowerPoint PPT presentation
Number of Views:122
Avg rating:3.0/5.0
Title: Quiz Answers
1
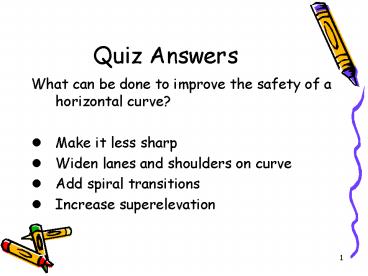
Quiz Answers
- What can be done to improve the safety of a
horizontal curve? - Make it less sharp
- Widen lanes and shoulders on curve
- Add spiral transitions
- Increase superelevation
2
Quiz Answers
- Increase clear zone
- Improve horizontal and vertical alignment
- Assure adequate surface drainage
- Increase skid resistance on downgrade curves
3
Some of Your Answers
- Decrease posted speed
- Add rumble strips
- Bigger or better signs
- Guardrail
- Better lane markers
- Sight distance
- Decrease radius
4
Superelevation and Spiral Curves
- CE 453 Lecture 18
5
Objectives
- Define superelevation runoff length and methods
of attainment (for simple and spiral curves) - Calculate spiral curve length
6
Other Issues Relating to Horizontal Curves
- Need to coordinate with vertical and topography
- Not always needed
MAXIMUM CENTERLINE DEFLECTION MAXIMUM CENTERLINE DEFLECTION
NOT REQUIRING HORIZONTAL CURVE NOT REQUIRING HORIZONTAL CURVE
Design Speed, mph Maximum Deflection
25 530'
30 345'
35 245'
40 215'
45 115'
50 115'
55 100'
60 100'
65 045'
70 045'
Source Ohio DOT Design Manual, Figure 202-1E Source Ohio DOT Design Manual, Figure 202-1E
7
Attainment of Superelevation - General
- Tangent to superelevation
- Must be done gradually over a distance without
appreciable reduction in speed or safety and with
comfort - Change in pavement slope should be consistent
over a distance - Methods (Exhibit 3-37 p. 186)
- Rotate pavement about centerline
- Rotate about inner edge of pavement
- Rotate about outside edge of pavement
8
Superelevation Transition Section
- Tangent Runout Section Superelevation Runoff
Section
9
Tangent Runout Section
- Length of roadway needed to accomplish a change
in outside-lane cross slope from normal cross
slope rate to zero
For rotation about centerline
10
Superelevation Runoff Section
- Length of roadway needed to accomplish a change
in outside-lane cross slope from 0 to full
superelevation or vice versa - For undivided highways with cross-section rotated
about centerline
11
Source A Policy on Geometric Design of Highways
and Streets (The Green Book). Washington, DC.
American Association of State Highway and
Transportation Officials, 2001 4th Ed.
12
Source A Policy on Geometric Design of Highways
and Streets (The Green Book). Washington, DC.
American Association of State Highway and
Transportation Officials, 2001 4th Ed.
13
(No Transcript)
14
Source CalTrans Design Manual online,
http//www.dot.ca.gov/hq/oppd/hdm/pdf/chp0200.pdf
15
Same as point E of GB
Source Iowa DOT Standard Road Plans
16
Attainment Location - WHERE
- Superelevation must be attained over a length
that includes the tangent and the curve (why) - Typical 66 on tangent and 33 on curve of
length of runoff if no spiral - Iowa uses 70 and 30 if no spiral
- Super runoff is all attained in Spiral if used
(see lab manual (Iowa Spiral length Runoff
length)
17
Minimum Length of Runofffor curve
- Lr based on drainage and aesthetics
- rate of transition of edge line from NC to full
superelevation traditionally taken at 0.5 ( 1
foot rise per 200 feet along the road) - current recommendation varies from 0.35 at 80
mph to 0.80 for 15mph (with further adjustments
for number of lanes)
18
Minimum Length of Tangent Runout
- Lt eNC x Lr
- ed
- where
- eNC normal cross slope rate ()
- ed design superelevation rate
- Lr minimum length of superelevation runoff (ft)
- (Result is the edge slope is same as for Runoff
segment)
19
Length of Superelevation Runoff
r
a multilane adjustment factor Adjusts for total
width
20
Relative Gradient (G)
- Maximum longitudinal slope
- Depends on design speed, higher speed gentler
slope. For example - For 15 mph, G 0.78
- For 80 mph, G 0.35
- See table, next page
21
Maximum Relative Gradient (G)
Source A Policy on Geometric Design of Highways
and Streets (The Green Book). Washington, DC.
American Association of State Highway and
Transportation Officials, 2001 4th Ed.
22
Multilane Adjustment
- Runout and runoff must be adjusted for multilane
rotation. - See Iowa DOT manual section 2A-2 and Standard
Road Plan RP-2
23
Length of Superelevation Runoff Example
- For a 4-lane divided highway with cross-section
rotated about centerline, design superelevation
rate 4. Design speed is 50 mph. What is the
minimum length of superelevation runoff (ft) - Lr 12ea
- G
24
- Lr 12ea (12) (0.04) (1.5)
- G 0.5
- Lr 144 feet
25
Tangent runout length Example continued
- Lt (eNC / ed ) x Lr
- as defined previously, if NC 2
- Tangent runout for the example is
- LT 2 / 4 144 72 feet
26
- From previous example, speed 50 mph, e 4
- From chart runoff 144 feet, same as from
calculation
Source A Policy on Geometric Design of Highways
and Streets (The Green Book). Washington, DC.
American Association of State Highway and
Transportation Officials, 2001 4th Ed.
27
Spiral Curve Transitions
28
Spiral Curve Transitions
- Vehicles follow a transition path as they enter
or leave a horizontal curve - Combination of high speed and sharp curvature can
result in lateral shifts in position and
encroachment on adjoining lanes
29
Spirals
- Advantages
- Provides natural, easy to follow, path for
drivers (less encroachment, promotes more uniform
speeds), lateral force increases and decreases
gradually - Provides location for superelevation runoff (not
part on tangent/curve) - Provides transition in width when horizontal
curve is widened - Aesthetic
30
Minimum Length of Spiral
- Possible Equations
- Larger of (1) L 3.15 V3
- RC
- Where
- L minimum length of spiral (ft)
- V speed (mph)
- R curve radius (ft)
- C rate of increase in centripetal acceleration
(ft/s3) use 1-3 ft/s3 for highway)
31
Minimum Length of Spiral
- Or (2) L (24pminR)1/2
- Where
- L minimum length of spiral (ft)
- R curve radius (ft)
- pmin minimum lateral offset between the
tangent and circular curve (0.66 feet)
32
Maximum Length of Spiral
- Safety problems may occur when spiral curves are
too long drivers underestimate sharpness of
approaching curve (driver expectancy)
33
Maximum Length of Spiral
- L (24pmaxR)1/2
- Where
- L maximum length of spiral (ft)
- R curve radius (ft)
- pmax maximum lateral offset between the
tangent and circular curve (3.3 feet)
34
Length of Spiral
- AASHTO also provides recommended spiral lengths
based on driver behavior rather than a specific
equation. See Table 16.12 of text and the
associated tangent runout lengths in Table 16.13. - Superelevation runoff length is set equal to the
spiral curve length when spirals are used. - Design Note For construction purposes, round
your designs to a reasonable values e.g. - Ls 147 feet, round it to
- Ls 150 feet.
35
Source Iowa DOT Design Manual
36
Source Iowa DOT Design Manual
37
Source Iowa DOT Design Manual
38
SPIRAL TERMINOLOGY
Source Iowa DOT Design Manual
39
Attainment of superelevation on spiral curves
- See sketches that follow
- Normal Crown (DOT pt A)
- Tangent Runout (sometimes known as crown runoff)
removal of adverse crown (DOT A to B) B TS - Point of reversal of crown (DOT C) note A to B
B to C - Length of Runoff length from adverse crown
removed to full superelevated (DOT B to D), D
SC - Fully superelevate remainder of curve and then
reverse the process at the CS.
40
Same as point E of GB
With Spirals
Source Iowa DOT Standard Road Plans RP-2
41
With Spirals
Tangent runout (A to B)
42
With Spirals
Removal of crown
43
With Spirals
Transition of superelevation
Full superelevation
44
(No Transcript)
45
Transition Example
- Given
- PI _at_ station 24574.24
- D 4º (R 1,432.4 ft)
- ? 55.417º
- L 1385.42 ft
46
With no spiral
- T 752.30 ft
- PC PI T 238 21.94
47
- For
- Design Speed 50 mph
- superelevation 0.04
- normal crown 0.02
- Runoff length was found to be 144
- Tangent runout length
- 0.02/ 0.04 144 72 ft.
48
- Where to start transition for superelevation?
- Using 2/3 of Lr on tangent, 1/3 on curve for
superelevation runoff - Distance before PC Lt 2/3 Lr
- 72 2/3 (144)
168 - Start removing crown at
- PC station 168 23821.94 - 168.00
- Station 236 53.94
49
Location Example with spiral
- Speed, e and NC as before and
- ? 55.417º
- PI _at_ Station 24574.24
- R 1,432.4
- Lr was 144, so set Ls 150
50
Location Example with spiral
- See Iowa DOT design manual for more equations
- http//www.dot.state.ia.us/design/00_toc.htmChapt
er_2 - Spiral angle Ts Ls D /200 3 degrees
- P 0.65 (calculated)
- Ts (R p ) tan (delta /2) k 827.63 ft
51
Location Example with spiral
- TS station PI Ts
- 24574.24 8 27.63
- 23746.61
- Runoff length length of spiral
- Tangent runout length Lt (eNC / ed ) x Lr
- 2 / 4 150 75
- Therefore Transition from Normal crown begins
at (23746.61) (075.00) 23671.61
52
Location Example with spiral
- With spirals, the central angle for the
circular curve is reduced by 2 Ts - Lc ((delta 2 Ts) / D) 100
- Lc (55.417-23)/4)100 1235.42 ft
- Total length of curves Lc 2 Ls 1535.42
- Verify that this is exactly 1 spiral length
longer than when spirals are not used (extra
credit for who can tell me why, provide a
one-page memo by Monday)
53
Location Example with spiral
- Also note that the tangent length with a spiral
should be longer than the non-spiraled curve by
approximately ½ of the spiral length used. (good
check but why???)
54
Notes Iowa DOT
Source Iowa DOT Standard Road Plans
Note Draw a sketch and think about what the last
para is saying












![Download Book [PDF] Paper Playground Books Presents Large Print Trivia Quiz for Adults, Seniors PowerPoint PPT Presentation](https://s3.amazonaws.com/images.powershow.com/10080312.th0.jpg?_=20240717015)

















