Aim: How do we transform functions? - 1 - PowerPoint PPT Presentation
1 / 27
Title:
Aim: How do we transform functions? - 1
Description:
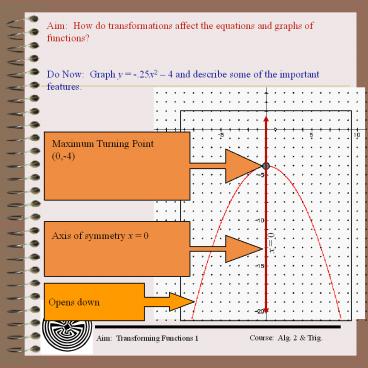
Aim: How do transformations affect the equations and graphs of functions? Do Now: Graph y = -.25x2 4 and describe some of the important features. – PowerPoint PPT presentation
Number of Views:136
Avg rating:3.0/5.0
Title: Aim: How do we transform functions? - 1
1
Aim How do transformations affect the equations
and graphs of functions?
Do Now Graph y -.25x2 4 and describe some
of the important features.
Opens down
2
Dilation of Parabola
In other words the absolute value of a, the
coefficient of x2, is a dilation factor that
changes the shape of the parabola
f(x) ax2 bx c
The absolute value of a determines fatness.
As the absolute value of a decreases in value,
the shape of the parabola gets fatter or wider.
As the absolute value of a increases, the shape
of the parabola gets thinner.
dilation Da
3
Translation of Parabola the c effect f(x)
ax2 bx c
In a quadratic equation c tells where the graph
crosses the y-axis.
The Nature of the Parabola
Translation T0,c
A(x, y) ? A(x, y c)
f(x) ? f(x) c
4
On the same set of axes, graph y .25x2 4 and
describe your results
Reflection of a parabola
y .25x2 4
Observations
Same turning point axis of symmetry
other symmetry?
y -4
y -.25x2 4
Each point on one graph is equidistant from the
line of reflection (y -4) as its image on the
other reflected graph.
5
Graph y -x2 6x 1 and reflect it about the
y-axis
x -6/2(-1) 3
-(0)2 6(0) - 1 -1 0,-1
-(1)2 6(1) - 1 4 1,4
-(2)2 6(2) - 1 7 2,7
-(3)2 6(3) - 1 8 3,8
-(4)2 6(4) - 1 7 4,7
-(5)2 6(5) - 1 4 5,4
-(6)2 6(6) - 1 -1 6,-1
Algebra of Reflection image of A(x,y) in the
y-axis is A(-x, y) image of B(x,y) in the
x-axis is B(x, -y) To graph find the
coordinates of the image of each of the seven
points under a reflection in the y-axis and
connect those points with a smooth line.
6
Graph y -x2 6x 1 and reflect it about the
y-axis
Image of A(x, y) in the y-axis is A(-x, y)
f(x) ? f(-x)
Reflection
(0,-1)
(0,-1)
(1,4)
(-1,4)
(2,7)
(-2,7)
(3,8)
(-3,8)
(4,7)
(-4,7)
(5,4)
(-5,4)
(6,-1)
(-6,-1)
Note axis of symmetry is also reflected under
the same rules
Algebra of Reflection image of A(x,y) in the
y-axis is A(-x, y) image of B(x,y) in the
x-axis is B(x, -y) To graph find the
coordinates of the image of key points under a
reflection in the y-axis and connect those points
with a smooth line.
What is the equation of the reflected parabola?
y -x2 6x 1
7
1.
2.
3.
4.
Which of the above graphs represent f(x) x2 1?
1
Which represents the image of the parabola
f(x) x2 1 under a reflection in the A.
x-axis B. y-axis C. The line y x D. The
line y -x
3
1
2
4
8
Graph the translation of y -x2 6x 1 under
a translation that maps (x, y) ? (x 2, y 1)
The image of every point on y -x2 6x 1 is
two units to the left and one unit up.
Algebra of Translation image of A(x, y) ? A(x
a, y b) a is the change in horizontal
unit distance and b is
the change in vertical unit distance To
graph find the coordinates of the image and
connect those points with a smooth line.
9
Vertex Form of Equations of Parabola
Graph the following parabola on the same set of
axes
y x2
y x2 5
y (x 3)2 - 5
y (x 5)2 - 5
y (x 7)2 1
Describe your findings
10
Vertex Form of Equations of Parabola
f(x) x2
Trans. Rule?
f(x) x2
A(x, y) ? A(x , y 5)
A(x, y) ? A(x 3, y 5)
A(x, y) ? A(x 5, y 5)
y x2 5
A(x, y) ? A(x 7, y 1)
f(x) (x h)2 k represents a
horizontal translation of f(x) x2, h units to
the right if h is positive or h units to left if
h is negative and a vertical translation of k
units. The coordinate (h, k) is the turning
point of the parabola.
11
Aim How do transformations affect the equations
and graphs of functions?
Do Now
Write the equation and sketch the graph of y x3
after a transformation that translates it 3 units
up.
after a transformation that translates it 3 to
the left.
after both a transformation that translates
it 3 units up and 3 to the left.
12
Vertical Horizontal Translations
- If k and h are positive numbers and
- f(x) is a function, then
- f(x) k shifts f(x) up k units
- f(x) k shifts f(x) down k units
- f(x h) shifts f(x) right h units
- f(x h) shifts f(x) left h units
f(x) (x h)2 k - quadratic
f(x) x h k - absolute value
f(x) (x h)3 k - cubic
f(x) (x h)4 k - quartic or 4th degree
ex. f(x) (x 4)2 4 is the image of g(x)
x2 after a shift of 4 units to the right and
four units up or a translation of T4,4.
13
Reflections of Functions
image of B(x,y) in the x-axis is B(x, -y)
Given f(x)
-f(x) is a reflection of f(x) through the x-axis
f(x)
(x 3)2 1
f(x) (x h)2 k - parabolic
(3, 1)
(h, k) is the turning point of the parabola.
-f(x)
-(x 3)2 1
14
Reflections of Functions
image of A(x,y) in the y-axis is A(-x, y)
Given f(x)
f(-x) is a reflection of f(x) through the y-axis
f(x)
f(-x)
(x 3)2 1
((-x) 3)2 1
15
Reflections of Functions
Under reflection in the origin, the Image of P(x,
y) ? P(-x, -y)
Given f(x)
-f(-x) is a reflection of f(x) through the origin
-((-x) 3)2 1)
f(x)
-f(-x)
(x 3)2 1
16
Dilations of Functions
Given f(x)
af(x) is a dilation of f(x) by a factor of a
If a gt 1, the function is stretched vertically
If a lt 1, the function is stretched horizontally
17
Transformation of Functions
Translation
Reflection
Dilation
f(x) (x h)n k n is integer gt 1
-f(x) is a reflection of f(x) through the x-axis
f(-x) is a reflection of f(x) through the y-axis
-f(-x) is a reflection of f(x) through the origin
af(x) is a dilation of f(x) by a factor of a
If a gt 1, the function is stretched vertically
If a lt 1, the function is stretched horizontally
18
Regents Prep
19
Model Problems
Graph y (x 1)2 5
20
Standard to Vertex Form
Rewrite the equation of a parabola in vertex
form. f(x) x2 4x 1
f(x) x2 4x 1
Separate the first two terms from c.
f(x) (x2 4x ) 1
Take 1/2 the coefficient of the b term, square it
then add the result to the terms inside the
parentheses and subtract it from the constant
outside.
f(x) (x2 4x ) 1
4 4
Rewrite the perfect square trinomial in the
parenthesis as a binomial square and add the
constants together.
f(x) (x 2)2 3
21
Translating Absolute Value Functions
Graph y x y x
3 y x 3
y x h represents a horizontal translation
of y x, h units to the left if h is positive
or h units to right if h is negative
22
Translating Absolute Value Functions
Graph y x
Graph y x 3 and y x 2
y x k represents a vertical translation
of y x, k units
23
Translating Absolute Value Functions
Graph y x 3 1
y x h k represents a horizontal shift of
h units to the right if h is positive or h units
to left if h is negative and a vertical
translation of k units
24
Translating Absolute Value Functions
standard form -
Graph y x 3
a 1, b 1, c -3, and d 0
Find the coordinate of the vertex by evaluating
bx c 0
bx c 0 ? 1(x) 3 0
x 3
Construct a table of values using the x-value of
the vertex and several values to the left and
right of it.
x x 3 y x,y
0
1
2
3
4
5
3 3 0,3
2 2 1,2
1 1 2,1
Graph the resulting points to form the V-shaped
graph
0 1 3,0
1 1 4,1
If a is positive V opens up
2 2 5,2
If a is negative V opens down
25
The Punted Football
- The height of a punted football can be
- modeled by the quadratic function
- h - 0.01x2 1.18x 2. The horizontal
distance - in feet from the point of impact is x, and h is
the - height of the ball in feet.
- a. Find the vertex of the graph of the function
- by completing the square.
- What is the maximum height of this punt?
- c. The nearest defensive player from the point
- of impact is 5 feet away. How high must he get
- his hand to block the punt?
26
The Punted Football
h - 0.01x2 1.18x 2
Really Small Peoples Football League
4
2
27
The Punted Football
h -x2 118x 200
Rewrite the quadratic for h 0
x2 118x 200
3481
3481
3481
x2 118x 200
(x - 59)2 3681
x - 59 60.67