A

1
B
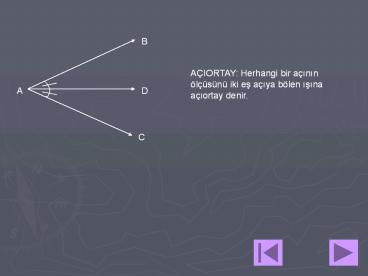
AÇIORTAY Herhangi bir açinin ölçüsünü iki es
açiya bölen isina açiortay denir.
A
D
C
2
A
Bir üçgende iç açiortaylar bir noktada
kesisirler. Bu noktada üçgenin iç teget
çemberinin merkezidir.
O
B
C
3
A
Açiortay dogrusu üzerindeki herhangi bir nokta
(P) dan açinin kenarlarina çizilen dik uzakliklar
birbirine esittir. Yani IPAI IPCI dir.
(açiortay dogrusu simetri ekseni oldugundan)
B
P
C
IPAI IPCI IBAI IBCI ve m(APB) m
(PBC) A(BAP) A(BPC) dir.
4
IÇ AÇIORTAY TEOREMI
A
b
c
m
n
B
C
N
IANI² b.c m.n
5
DIS AÇIORTAY TEOREMI
A
c
b
B
N
y
C
x
ABC üçgeninde AN, BAC nin dis açiortayi olmak
üzere
IACI
INCI
b
x
gt
bagintisi vardir.


c
xy
IABI
INBI
IANI² x(xy) b.c formülüyle bulunur.
IANI ise
6
ÖRNEK
A
3
D
C
B
8
ABC bir diküçgen AB
AC
BD iç açiortay IADI 3 cm IBCI
8cm Verilenlere göre A(BDC) ?
7
ÖRNEK
ABC bir diküçgen AB AC CD iç açi
ortay IBCI IACI 2 IADI 4 cm IBDI
x Verilenlere göre x?
-
A
4
D
x
C
B
8
ÖRNEK
A
10
8
B
C
N
9
ABC bir üçgen AN iç açiortay IABI 8cm IBCI
9cm IACI 10cm IANI ?
9
ÖRNEK
A
ABC bir diküçgen AN iç açi ortay IBNI
2cm INCI 3cm
x
Verilenlere göre IACI ?
B
C
3
2
N
10
ÖRNEK
A
3
2
B
N
4
C
ABC üçgeninde AN dis açiortay IACI 2 cm IABI
3 cm IBCI 4 cm
Verilenlere göre IANI ?
11
ÖRNEK
A
x
4
B
N
C
ABC bir üçgen AN dis açiortay A(ABC)
9cm² A(ACN) 12cm² IACI 4cm IABI ?
12
ÖRNEK
A
ABC bir diküçgen AD iç açiortay m(ACB)
45º IBDI 2cm IDCI ?
B
45
C
x
2
N
13
ÖRNEK
ABD bir üçgen AC iç açiortay IACI IADI ICDI
2 cm IBCI 3 cm IABI ?
A
x
2
3
B
C
D
14
ÖRNEK
A
ABC bir üçgen M(BAD) B (DAC) 15º IABI 10
cm IACI 15 cm A(ABD) ?
15º
15º
10
15
B
C
D
15
ÖRNEK
ABC bir üçgen AD dis açiortay AC
BD IBCI 9 cm IABI 15 cm ICDI ?
A
-
15
B
C
D
9
x
16
ÇÖZÜM
A
3
D
BD, açiortay oldugundan D noktasindan çizilen
dik uzakliklar esittir.
3
C
H
B
8
Yani IADI IDHI 3cm olur. Dolayisiyla A(DBC)
8x3 / 2 12cm²
17
ÇÖZÜM
A
4
a
D
x
B
H
C
a
2
CD açiortay oldugundan D noktasindan BC ye
çizilen dikme Ad ye esit olur. IDHI IADI
4cm olur. Açiortay dogrusu simetrik oldugundan
IACI IHCI a dersek, IBCI a 2 olacagindan
IBHI 2cm olur. DBH diküçgeninde pisagor
bagintisindan x² 4² 2² , x 2v5
18
ÇÖZÜM
ABC üçgeninde INCI x dersek IBNI 9-x olur.
A
10
8
8
10

x
9-x
Buradan x 5cm bulunur.
B
C
9-x
x
N
Iç açiortay teoreminden IANI² 8.10 4.5 IANI²
60 IANI 2v15
19
ÇÖZÜM
A
Iç açiortay teoreminden IABI
2
oldugundan

IACI
3
x 3a
a
IABI 2a IACI 3a dersek
B
C
3
2
N
ABC üçgeninde pisagor bagintisindan IACI² IABI²
IBCI² (3a)² (2a)² 5² Buradan a v5 O
halde IACI 3a 3v5
20
ÇÖZÜM
A
3
2
B
N
4
C
x
IACI
INCI
2
x


gt
gt
x 8cm bulunur
IABI
INBI
3
x4
Dis açiortay ise IANI² x(x4) 2.3 IANI²
90 IANI 3v10
21
ÇÖZÜM
A
x
4
Yükseklikleri ayni olan üçgenlerin alanlari orani
tabanlari oranina esittir.
9
12
B
N
C
A(ABC) IBCI 9 3



IBCI 3a, ICNI 4a dersek IBNI7a
A(ACN) ICNI 12 4
IACI
INCI
4
4a

gt

gt
x 7cm
IABI
INBI
x
7a
22
ÇÖZÜM
A
AD iç açiortay oldugundan D noktasindan AC ye
çizilen dikme BD ye esit olur. IBDI IDHI
2cm
H
B
45
45
DHC üçgeni ikizkenar diküçgen oldugundan x 2v2
cm bulunur.
C
x
2
N
23
ÇÖZÜM
A
ABC üçgeninde AC iç açiortay oldugundan
3a x
2a
2a
IABI
3

dir.
IADI
2
2
3
B
C
D
IABI 3a, IADI 2a dersek IACI IADI 2a
olur. Iç açiortay formülünden (2a)² 3a.2a
3.2 4a² 6a² - 6 gt 2a² 6
a v3 olur. IABI 3a 3v3
bulunur.
24
ÇÖZÜM
A
AD iç açiortay oldugundan
IABI
IBDI
10
2
15º

15º


IACI
15
3
IDCI
10
15
IBDI 2a, IDCI 3a dersek A(ABD) 2S, A(ADC)
3S, A(ABC) 5S olur.
B
C
D
1
1
A(ABC) .10.15.sin30 gt 5S
10.15.0,5
2
2
75
15
5S cm² gt S cm²
2
2
15
A(ABD) 2S 2.

15 cm²
2
25
ÇÖZÜM
A
ABC diküçgeninde pisagor bagintasindan IACI²
IBCI² IABI² IACI² 9² 15² IACI² 144 IACI
12 cm bulunur.
15
B
C
D
9
x
Dis açiortay teoreminden
IACI
IDCI
12
x



gt x 36 cm bulunur.
IABI
IDBI
15
x 9