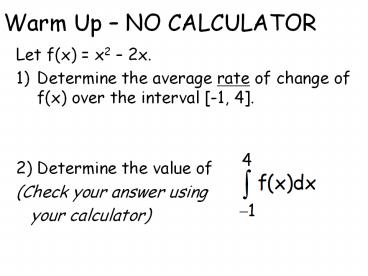Warm Up

1
Warm Up NO CALCULATOR

• Let f(x) x2 2x.
• Determine the average rate of change of f(x) over
  the interval -1, 4.
• Determine the value of
• (Check your answer using
• your calculator)

2
Mean Value Theorem for IntegralsAverage
Value2nd Fundamental Theorem of Calculus
3
Mean Value Theorem for Integrals If f is
continuous on a,b then there is a certain point
(c, f(c)) between a and b so if you draw a
rectangle whose length is the interval a,b and
whose height is f(c), the area of the rectangle
will be exactly the area beneath the function on
a,b.
4
In other words

• If f is continuous on a,b, then there exists a
  number c in the open interval (a,b) such that .

Area under the curve from a to b
Area of the rectangle formed
5
Example 1

• Find the value of f(c) guaranteed by
  
• the MVT for Integrals for the function
• f(x) x3 4x2 3x 4 on 1,4

Explain the relationship of this value to
the graph of f(x)?
6
Example 2

• Find the value of f(c) guaranteed by the MVT for
  Integrals on the interval 1,9 for

7
The f(c) value you found in both examples is
called the average value of f.
Solving for f(c) gives the formula for average
value.
8
Example 3
Find the average value of f(x) 3x2 2x on the
interval 1,4 and all values of c in the
interval for which the function equals its
average value.
9
Taking the derivative of a definite integral
whose lower bound is a number and whose upper
bound contains a variable.
10
Your turn
11
(No Transcript)
12
6) If
13
Let f be defined on the closed interval -5,5.
The graph of f consisting of two line segments
and two semicircles, is shown above.
f
14
Let g be the function given by
f
Find g(2)
Find g(2)
Find g(2)
15
g(x)
f
a. On what intervals, if any, is g increasing?
b. Is x -3 a relative max or a relative min
of g(x)?
c. Find the x-coordinate of each point of
inflection of the graph g on the open
interval (-5,5). Justify your answer.