Public%20Key%20Cryptosystem PowerPoint PPT Presentation
Title: Public%20Key%20Cryptosystem
1
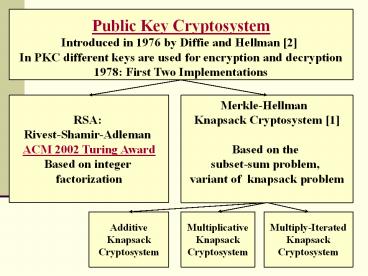
Public Key Cryptosystem Introduced in 1976 by
Diffie and Hellman 2 In PKC different keys are
used for encryption and decryption 1978 First
Two Implementations
RSA Rivest-Shamir-Adleman ACM 2002 Turing
Award Based on integer factorization
Merkle-Hellman Knapsack Cryptosystem
1 Based on the subset-sum problem, variant
of knapsack problem
Additive Knapsack Cryptosystem
Multiplicative Knapsack Cryptosystem
Multiply-Iterated Knapsack Cryptosystem
2
Public Key Cryptosystems
- Elliptic curve cryptography (ECC) is an approach
to PKC based on the algebraic structure of
elliptic curves over finite fields. The use of
elliptic curves in cryptography was suggested
independently by Neal Koblitz and Victor S.
Miller in 1985. - The NTRUEncrypt public key cryptosystem, also
known as the NTRU encryption algorithm, is a
lattice-based alternative to RSA and ECC and is
based on the shortest vector problem in a
lattice.
3
Public Key Cryptosystems
- ElGamal encryption system is an asymmetric key
encryption algorithm for PKC which is based on
the DiffieHellman key exchange. It was described
by Taher Elgamal in 1985. - The Digital Signature Algorithm (DSA) is a United
States Federal Government standard or FIPS for
digital signatures.
4
Links
- http//www.nytimes.com/keyword/adi-shamir
- http//simson.net/ref/1988/Landau_Zero_Knowledge.p
df - http//en.wikipedia.org/wiki/Public-key_cryptograp
hy - http//en.wikipedia.org/wiki/Zero-knowledge_proof
5
RSA
Alice 1. Chooses secret (private) key 2. Create
and publishes public key 3. Receives ciphertext
from Bob 4. Decrypts ciphertext using secret key
to recover the plaintext original message
Bob 1. Uses Alice Public Key to encrypt the
message 2. Sends ciphertext encrypted message
to Alice
6
ALICE Preparation Step Creates Private and
Public Key
- Selects two primes p and q
- Calculates
- m pq
- n ( p 1 ) ( q 1 )
- Selects e that relatively prime to n, gcd (e, n )
1 - Finds the multiplicative inverse of e mod n.
Denotes the multiplicative inverse by d - ed ? 1 (mod n)
- Publishes e and m this is the public key
7
BOB - Encryption
- Plaintext is number x
- 0 ? x ? m -1
- gcd (x, m) 1
- Ciphertext y is calculated as follows
- y xe mod m
- y is sent to Alice
8
Alice - Decryption
- Alice receives the ciphertext y
- Calculates yd mod m and this is a plaintext x,
so the final formula is x ? yd ( mod m ) - Why is it working?
- e-1 ? d ( mod n ) means ed ? 1 (mod n) means
- ed 1 kn 1 k ( p -1 )( q -1 ) (for some
integer k ) - yd ? (xe mod m )d ? xed ? x 1 k(p-1)(q-1) ? x
(mod m) (Theorem 4.3.2 from your textbook, x
has to be relatively prime to m pq)