Arithmetic Expressions and Built in Functions

1
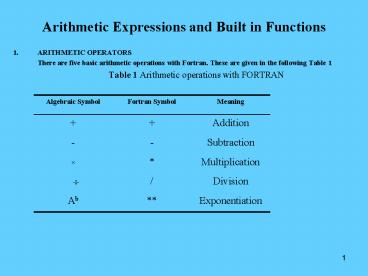
Arithmetic Expressions and Built in Functions

• ARITHMETIC OPERATORS
• There are five basic arithmetic operations with
  Fortran. These are given in the following Table 1
• Table 1 Arithmetic operations with FORTRAN

Algebraic Symbol Fortran Symbol Meaning
Addition
- - Subtraction
Multiplication
/ Division
Ab Exponentiation
2

• 2. ARITHMETIC EXPRESSION
• Arithmetic expressions are formed either by
  combining integer
• variable names and constants with arithmetic
  operators or by combining real
• variable names and constants with arithmetic
  operators. Thus, in Fortran, two
• types of expressions are defined.
• i) Integer Expression e.g. I, L, 8, -7,
  NM, MNI, (IJ) / (IK)I etc.
• Real Expression e.g. A, -A, 4.2, 1.5,
  -ABCD, (AB), (A4.5), (AB) /(DC) etc.
• Note If expression consists of integer/real
  variables then it is called Mixed Mode
  expression e.g.
• 20IX3, (AB) (KJ) etc.

3

• 3 (a) Integer arithmetic
• If the operands are integers, then integer
  arithmetic is performed to yield an integer.
• e.g. 53 yields 8
• 53 yields 15
• 5-3 yields 2
• Integer division in FORTRAN, also yields an
  integer- the integral part of the quotient only
  i.e. the fractional part of the quotient is
  deleted in integer division.
• e.g. 5/4 yields 1
• 4/5 yields 0
• -7/2 yields -3
• Exponent of integer number/variable can only be
  integer
• e.g I2 I 2 (Valid)
• I2.0 (Invalid)
• 3(b) Real arithmetic
• If the operands are real, the real arithmetic is
  performed to yield a real value.
• e.g. 5.03.0 yields 8.0
• 5.3. yields 15.
• 5.0-3.0 yields 2.0 etc.

4
Division by real arithmetic in FORTRAN is similar
to ordinary division, e.g. 5.0/4.0 yields
1.25 4.0/5.0 yields 0.8
etc. Exponent of real number/variable can be
integer/real. e.g. If we have expression, z x
y x y, then it is solved as i) If y is
real Taking log on both sides, log z y log
x Taking antilog, z antilog (y log x) e y
log x exp (y log x) ii) If y is an integer,
then x y is evaluated by repeated
multiplication. Now, if we want to solve
(3.2)7then if we write, 3.2 7.0, then log and
antilog will be used by the computer. If we
write, 3.2 7, then simple multiplication will
take place. Since, logs takes more computation
time as compared to multiplication, hence
exponent should be kept real only if it contains
fractional part too, otherwise keep the exponent
integer.
5

• 4. HIERARCHICAL RULE FOR THE OPERATONS IN
  THE EXPRESSIONS
• The order, in which arithmetic operations are
  executed in an expression, is called the
  hierarchy or precedence of operations.
• Table. 2 shows the precedence priority of
  operators.

6

• Table 2 Precedence of Operators

Priority Fortran Symbol Meaning/Operation
1. ( ) Parenthesis
2. Exponentiation
3. / Multiplication, Division
4. - Addition, Subtraction
7
Rule 1. All expressions in parentheses are
evaluated first. Rule 2. Operators in the same
expression are evaluated according to the
hierarchy followed by , / followed by , -.
Rule 3. If priority of two operators are equal,
then expression is scanned from left to right
whichever operator (of same priority) comes first
will be operated first. Rule 4. Priority of
operators can be changed by using parentheses.(
Expression within parentheses is to be solved
first by applying Rule 1 and Rule 2). Rule
5. Parentheses can be nested also. The inner most
parentheses is to be solved first and then next
outer and so on.
8
Example 1 Consider an expression X 68.0 Y
Z/ (A-8.7) Following Hierarchical Rule, the
solution will be in the steps shown
9

• Example 2. Let us now consider the solution of an
  expression
• X Y Z/ (IJ) (I (J/4))
• where X,Y and Z are real variables and I and J
  are integer variables.
• This expression is evaluated in following steps
  with mixed mode as shown below.

10
Example 3. The expression x y/ (ZAB2) is
evaluated as follows,
Example 3. The expression x y/ (ZAB2) is
evaluated as follows,
x y
/
(ZA
B2)

/
11

• Note Parenthesis can be used to make the
  expression more clear.
• By using the parenthesis we can alter the
  precedence of operation
• e.g. in b4a / b a the precedence is
• but in the expression, b4a / (b a) the
  precedence (of (ba)) changes as shown below

12
e.g (i) The expression , AB
is written as, A B
(C/D) GA/(5B3) (ii) The expression,
is written as,
A/(BC) D2
13

• BUILT IN FUNCTIONS
• Built in functions are also known as LIBRARY
  FUNCTIONS OR INTRINSIC FUNCTIONS.
• These are the pre-written programs by the
  manufacturer of the compiler, for commonly used
  mathematical functions.
• These functions can be called, in users program
  by writing the name of the function-program and
  enclosing the argument in the parentheses
• Example SQRT (X) , ABS (X)
  
• ALOG (X) loge X etc.
• Points to Remember (while using
  Built-in-functions in the Program)
• The argument should be enclosed in parentheses.
• If a function has more than one argument, then
  arguments should be separated by commas.
• Care should be taken to match
• - the type
• - the number and
• - the order of arguments..
• Most common functions used in FORTRAN have been
  summarized in Table 3.

14
Table 3.
Function Mathematical Notation FORTRAN
Square root of x SQRT (X)
Absolute value of x ABS (X)
Exponential of x ex EXP (X)
Sine of x sin x SIN (X)
Cosine of x cos x COS (X)
Tangent of x tan x TAN (X)
Inverse of sine sin-1 x ASIN (X)
Inverse of cosine cos-1 x ACOS (X)
Inverse of tangent tan-1 x ATAN (X)
Log of x log10 x ALOG 10(X)
Natural log of x loge x ALOG (X)
Convert integer Into real FLOAT (I)
Truncate real x into integer I FIX (X)
Give only quotient These two functions are DIV (I,J)
Give only remainder Used only for integers. MOD (I,J)
15

• e.g- (i) an expression is written as
• SQRT (SQRT ((A-B) /
  (C4D)))
• (ii) The expression is written as
• A (C-1) / ALOG (B)
• (iii) The expression tan-1 is written
  as
• ATAN (SQRT (Sin (ABS
  (A))2))
• iv) The exp e b tan3 a is written as
  EXP (B) TAN (A)3
• .

16
6. EXECUTABLE AND NON-EXECUTABLE
STATEMENTS Executable Statements These are the
statements which result in a machine code i.e.
which result in some kind of machine-language
instruction . For example, READ, WRITE, STOP,
GOTO, IF, DO etc. Non-Executable Statement
These are the statements which do not result in
any machine code i.e. which will not result in
any machine-language instructions. For example
COMMENT statements, TYPE statement, FORMAT,
TYPE, END, ELSE, COMMON, DIMENSION etc. Note
STOP is an executable statement. Its machine
language equivalent stops the computer from
executing the next machine language instruction
of the program. END is a non-executable
statement. It tells the compiler that this is the
end of the program and there are no more FORTRAN
statements to be transferred into machine
language instructions.