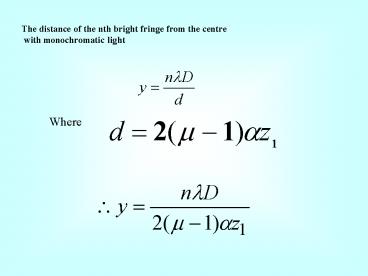The distance of the nth bright fringe from the centre

1
The distance of the nth bright fringe from the
centre with monochromatic light
Where
2
c
A
E
Fringes of equal width
S
d
a
F
B
Fringes of large width
Z2
Z1
b
D
3
(No Transcript)
4
For green light,
For red light,
5
(No Transcript)
6
A Transparent material G of thickness t and
refractive index ? is placed in the path of one
beam.
WHAT WILL HAPPEN?
7
G
8
Fringe pattern will remain same
or
Interference fringe pattern will shift
9
Light wave from S2 will go directly to P but
light wave from S1 will go to P partly through
air and partly through Transparent material G.
Time required for the light to reach from S1 to
the point P is
C0 is the velocity of light in air and C its
velocity in the medium
By introducing thin plate the effective optical
path changes.
10
The time needed for both the path will be same.
.(1)
11
Time required for the light to reach from S1 to
the point P is
Clearly effective path in air from S1 to P is S1P
(?-1)t
12
So the air path S1P has been increased by S1P
(?-1)t as a result of the introduction of the
plate.
.(1)
13
So the path difference between the beams
reaching P, from S1 and S2 (?)
If there is no transparent plate then we know the
path diff
14
So the path difference will be
If P is the centre of the nth bright fringe, then
15
At n 0 the shift y0 of central bright fringe is
It means that the introduction of the plate in
the path Of one of the interfering beams
displaces the entire Fringe system through a
distance
This displacement is towards the beam in the path
of which The plate is introduced.
16
So central fringe at C is shifted from C to point
P on The screen on insertion of transparent plate
material Of refractive index ?
Knowing the distance through which the central
fringe is shifted, D, d and ? the thickness of
the material t can be calculated.
17
We have to use white light to determine the
thickness of the material.
For monochromatic light central fringe will
similar to other bright bright fringe. For white
light central fringe is white.
18
THE LLOYDS MIRROR ARRANGEMENT
L
L
19
Light directly coming from the slit S1interferes
with the light reflected from the mirror forming
an Interference pattern in the region BC of the
screen.
For two sources one is real and the other one is
virtual.
20
The central fringe will be dark.
Reflected beam undergoes a sudden phase change of
? On reflection.SO at
S2P S1P n?
We can get minima (destructive interference)
S2P S1P (2n1)?/2
and
We get maxima (constructive interference)
21
Using the principle of optical reversibility
we Can say that there will be an abrupt phase
change Of ? when light gets reflected by the
denser medium
No such phase change occurs when reflection
takes Place at rarer medium.
22
Phase change on Reflection, Refraction
23
Principle of optical reversibility
In the absence of any absorption, a light ray
that is reflected or refracted will retrace its
original path if its direction is reversed.
24
a ? amplitude of incident ray
r1 ? reflection coefficient
t1, ? transmission coefficient
n1
o
n2
n2gtn1
fig1
25
r1, r2 ? reflection coefficients
t1, t2 ? transmission coefficients
n1, n2 ? refractive index of two media
n2gtn1
a ? amplitude of incident ray
ar ? amplitude of reflected ray
at ? amplitude of refracted ray
26
ar12
ar1
at1t2
n1
I
at1r2
II
n2
at1
at1r1
fig2
27
According to principle of optical
reversibility the two rays of amplitudes ar12 and
at1t2 must combine to give the incident ray of
fig 1.
So,
ar12 at1t2 a
Stokes relation
? t1t2 1- r12
(1)
The two rays of amplitudes at1r1 and at1r2
must cancel each other.
So, at1r1 at1r2 0
(2)
? r2 -r1
Stokes relation
28

• Relation (2) represents that the coefficient of
  reflection from the surface of a denser medium is
  equal in magnitude to the coefficient of
  reflection from the surface of a rarer medium but
  opposite in sign.
• Intensity of reflected light is the same for a
  ray incident from either side of the boundary.
• Negative sign in amplitude indicates a phase
  change of ? occurring due to reflection at medium
  I and II. There are two possibilities
• If there is no phase change on reflection at
  medium I, there must be a phase change of ? on
  reflection from medium II.
• If there is no phase change on reflection from
  medium II, there must be a phase change of ? on
  reflection from medium I.
• Equation (2) does not give any information as to
  which of the two reflection gives the phase
  change.

29
Phase change ? occurs when light gets
reflected from denser medium.
? LLOYDS MIRROR
From equation (2) we may say that no phase change
will occur when light gets Reflected by a rarer
medium.
or

• There is no phase change on reflection from
  medium II, there must be a phase change of ? on
  reflection from medium I.

30
Interference in thin films due to reflection
31
Colours of oil film on water
Colours of soap bubble
Interference of thin film
Interference by division of amplitude
32
II
I
d
a
c
b
DIVISION OF AMPLITUDE
33
If plane wave falls on a thin film then the
wave reflected from the upper surface interferes
with the wave reflected from the lower surface.
Thin films are material layers of about 1 µm
thickness. For thin-film optics, the thickness of
the layers of material must be on the order of
the wavelengths of visible light. Layers at this
scale can have remarkable reflective properties
due to light wave interference.
34
Q
H
L
K
E
i
S
? gt 1
i
i
P
N
r
O
F
L
35
The optical path difference between the rays PQ
and EH is
X ?(PF FE) PK X ?(PNNFFE) - PK
Here ltSPL ltLPK i
In ? EKP, ltKPE lt90?-i ltEKP
lt90? so, ltKEP i
Similarly in ? PNE, lt PEN r
36
Now, PK ? PN
? X ? (PNNFFE)-?PN X ?(NFFE)
37
Q
H
K
E
i
r
S
? gt 1
i
i
P
J
N
r
r?
C
O
F
?
R
r?
L
38
EC is normal to OA.triangles ECF and FCL are
congruent.
EC CLt and FE FL X ? (NFFL) ? NL
..(i)
Angle between the inclined surfaces is the same
as the angle Between the normals at P and F.
SO, ltPRF ?
Again the exterior angle ltPEJ of ? PRF is equal
to the sum of the interior angles,
ltPEJ r ?
39
Now JR and EL are parallel and PEL cuts these
parallel lines
Such that ltFLC ltNFJ r ?
In right angled triangle ENL , COS
(r ?) NL/EL NL EL COS (r
?) NL 2t COS (r ?)
From equ (i), x 2?t COS (r
?)
40
Since PQ is the reflected wave train from a
denser medium Therefore there occurs a phase
change of ? or a path Difference of ?/2.
Effective path difference between the interfering
waves PQ and EH is ?
2 ?tcos(r?)-?/2
41
Condition for constructive interference
2 ?tcos(r?) - ?/2 n? 2 ?tcos(r?) (2n1) ?/2
(1)
Condition for destructive interference
2 ?tcos(r?)n? (2)
42
From equ (1) and (2)
So bright and dark fringes of different orders
will be observed at different thickness of the
film.
Practically ? is very small , therefore Cos(r
?)?cosr and so the condition will be
2 ?tcosr(2n1) ?/2
2 ?tcosrn?
and
43

• For monochromatic light beam incident on a wedge
  shaped film ?, ? are constant. So change in path
  difference is only due to varying thickness of
  the film. At a particular point thickness is
  constant. So we get a bright or dark fringe at
  that point due to constant path difference.
• Thickness of the film continuously changes. So
  equidistant interference fringes are observed
  parallel to the line of intersection of the two
  surfaces means parallel to the edge of the wedge .

44
Q
H
K
E
i
r
S
? gt 1
i
i
P
J
N
r
r?
C
O
F
?
R
r?
L
45
B
Pnm
Pn1
Pn
?
A
Qn
Qn1
Qnm
C
x
Suppose nth bright fringe at Pn.
Thickness of airfilm will be at Pn PnQn tn
Relation for bright film will be 2 ?tn
cos(r?)(2n1) ?/2
46
For nearly normal incidence cosr 1
2 ?tn(2n1) ?/2 2 ? PnQn (3)
Next bright fringe will appear at Pn1 for n1th
fringe
2?Pn1Qn1 2(n1)1 ?/2..(4) 2?tn1
2(n1)1 ?/2
Subtracting (3) from (4)
2?Pn1Qn1 - 2 ? PnQn ? Pn1Qn1 PnQn
?/2? tn1 tn ?/2?
For air film Pn1Qn1 PnQn ?/2
47
Pn1Qn1 PnQn ?/2
So next bright fringr will appear where air
thickness will increase by ?/2.
For (nm) th bright fringe
PnmQnm PnQn m?/2 tnm tn m?/2
Therefore let at x distance from Qn m th bright
fringe appears then
48
Pnm
Pn1
PnmQnm PnQn
Pn
L
?
x
?
A
Qn
Qn1
Qnm
C
For small ?
Fringe width
49
eye
B
Air film
?
A
O
C
O
The interfering rays do not enter the eye
parallel to each other but they appear to diverge
from a point near the film.