18_12afig_PChem.jpg PowerPoint PPT Presentation
1 / 50
Title: 18_12afig_PChem.jpg
1
18_12afig_PChem.jpg
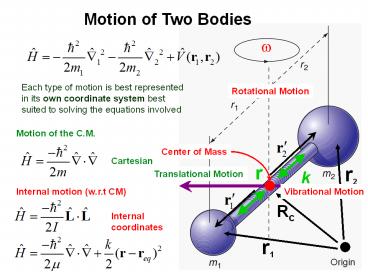
Motion of Two Bodies
w
Each type of motion is best represented in its
own coordinate system best suited to solving the
equations involved
Rotational Motion
Motion of the C.M.
Center of Mass
Cartesian
r2
r
k
Translational Motion
Internal motion (w.r.t CM)
Vibrational Motion
Rc
Internal coordinates
r1
Origin
2
Motion of Two Bodies
Centre of Mass
Weighted average of all positions
Internal Coordinates
In C.M. Coordinates
3
Centre of Mass Coordinates
4
Hamiltonian
Separable!
C.M. Motion 3-D P.I.B
Internal Motion Rotation Vibration
5
18_11fig_PChem.jpg
Simple Harmonic Motion
Conservation of Energy
Still
fast
Still
Kinetic Energy
Max
Max
V
Potential Energy
K
Min
Min
Hooks Law
6
18_01fig_PChem.jpg
Hamiltonian of a Diatomic
r
k
Symmetric
Can be approximated by a quadratic
Harmonic Approx.
Odd
Odd
Even
7
Hamiltonian of a Diatomic
Radial
Angular
8
Hamiltonian of a Diatomic
Assuming
9
Hamiltonian of a Diatomic
Consider
This DE can be solved using Power series method,
or using ladder operators
10
Vibrational Wavefunctions
Hermite polynomials
Oscillation
Highly excited state n12
Gaussian
Tunneling
11
Solving the Schroedinger Equation
Reparameterize x r -re and dr dx
12
Ladder Operators
if
Recall
Otherwise
Just like with angular mom.
13
Ladder operators
Recall
Just like with angular mom.
This means that the lowest energy state has
non-zero energy
14
Ladder Operators
they share the same eigen functions
where
What does B do??
Consider
is the raising operator
Since
Similarly
is a lowering operator as
15
Hamiltonian of a Diatomic
The quantum number increases and decreases in
units of 1.
However l must have a lowest allowable value,
since the energy has to be positive, i.e. E gt 0.
Consider
with eigenvalue
since
16
Hamiltonian of a Diatomic
Similarly one can show that
17
Derivation of Ground State Wavefunction
Not normalized
18
lmin is an Eigenfunction of the Hamiltonian
19
Normalization of 1D GS WF
20
Expectation values of 1D GS WF
Virial Theorem ltKgt E/2
This indicates of the variance of the
distribution of the WF. Ie. where the
standard deviation is
21
Higher Level Eigenfunctions of the Hamiltonian
Not normalized
22
Vibrational Wavefunctions
23
Normalization of 3D WFs
Recall
where r gt 0
Normalization
24
Normalization of 3D WFs
For typical values of a and re.
Therefore 1D and 3D results are essentially
equivalent
25
Expectation Values of 3D WFs
For typical values of a and re.
Therefore 1D and 3D results are essentially
equivalent
26
19_01fig_PChem.jpg
Spectroscopy
27
19_02tbl_PChem.jpg
Vibrational Spectroscopy
r(t)
D(t)
Band structure
28
19_10fig_PChem.jpg
Polyatomic Vibrations
For an N atom molecule
Total of 3N Coordinates (x,y,z)
3 CM Coordinates (X,Y,Z)
3 Axes of Rotation
Remaining coordinates are Vibrational modes
Normal modes have a characteristic frequency,
wi,determined by the motion they represent, and
are independent of each other
29
19_04tbl_PChem.jpg
Vibrational Spectra of Molecules
30
Vibrational Spectroscopy
Selection Rule
For perfect Harmonic Behaviour
E(n)
1st Overtone
not exactly 2x due to anharmonicity
2nd Overtone
31
19_p08_PChem.jpg
Selection Rules and Line Intensities
Boltzmann Distribution
At ambient T, most are in the ground state
ex) k 250 N/m, m 2x10-26 kg and T 298 K
0.003
E(n)
0.06
0.3
5.4
94
x
32
19_02tbl_PChem.jpg
Coupled Modes
Mode i
Combination Mode
Difference Mode
Fermi Resonance
Mode j
Causes linebroadening, and splitting
33
Rotation-Vibration Spectroscopy
34
Rotation-Vibration Spectroscopy
P Branch
R Branch
P Branch
R Branch
re
1H35Cl
2906.21
2925.83
2944.86
1.324 A
2865.00
1H37Cl
2904.22
2923.78
2942.79
1.323 A
k 480.58 N/m
R Branch
P Branch
2800
2900
3000
3100
2700
35
19_18fig_PChem.jpg
Instrumentation
Scanning
q
I
I0
Absorption
Grating Orientation (q)
36
19_18fig_PChem.jpg
Instrumentation
The reference and sample beams are coherent,
therefore they can interfere with each other.
The phase of the reference beam can be modulated
by changing the mirror position
Spectrum
FT
Inteferogram
Mirror Displacement
37
First Order Perturbation Theory
small
small
small
small
small
38
First Order Perturbation Theory
zero order
2nd order
Since the perturbation is small
2nd order
zero order
2nd order
zero order
Only 1st order terms remain
39
First Order Perturbation Theory
Project onto jth eigenstate of Ao
40
First Order Perturbation Theory
Case 1
Case 2
41
First Order Perturbation Theory
Close, however higher order corrections will be
needed
42
First Order Perturbation Theory
Not normalized
43
First Order Perturbation Theory in QM
44
Higher Order Perturbation Theory
45
The Anharmonic Oscillator
Odd
Odd
Even
46
The Anharmonic Oscillator
1st Oder Corrected Energy
Even
Odd
47
The Anharmonic Oscillator
48
The Anharmonic Oscillator
odd
Consider the Ground state
even
odd
odd
even
odd!!!
49
The Anharmonic Oscillator
50
The Anharmonic Oscillator