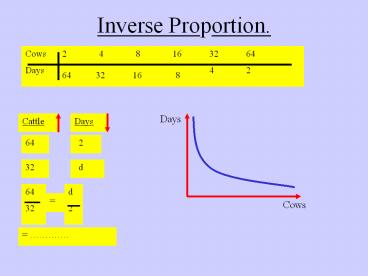
Inverse Proportion.

1
Inverse Proportion.
2
What Is Inverse Proportion ?
Consider the problem below
Problem 1.
A farmer has enough cattle feed to feed 64 cows
for 2 days.
(a) How long would the same food last 32 cows ?
4 days
(b) Complete the table below for the same amount
of cattle feed
8
16
32
64
We can now see what Inverse Proportion is all
about
3
Look at the cattle feed problem again
If you double the number of cows , what happens
to the number of days you can feed them ?
The number of days is halved.
If you treble the number of cows , what happens
to the number of days you can feed them ?
You can only feed them for a third of the number
of days.
If you have ten times the number of cows , what
happens to the number of days you can feed them ?
You can only feed them for a tenth of the number
of days.
For Direct Proportion when one quantity is
doubled , trebled quadrupled etc the other
quantity becomes a half , third, quarter etc.
4
There is another important fact to pick up on in
the table
What do you notice happens if you multiply cows x
days ?
Cows x days 128 for all pairs of values in the
table.
This gives us one method for solving Inverse
Proportion problems.
To see this method complete the problem below
Problem 2 .
It takes 96 hours for 3 strawberry pickers to
clear a field . Complete the table below
48
24
12
6
5
The Idea of Picker-Hours.
Using the table we have just completed we can now
find out how many hours any number of pickers
will take.
How many hours will 17 pickers take to complete
the job ?
Solution.
For all pairs of values
Pickers x hours 288 picker hours.
That is to say there are 288 hours of work to
complete.
Divide these hours amongst our 17 pickers
No of hours 288 ? 17 16.94 hours per picker.
It will take 16 hours and 57 minutes to the
nearest minute.
6
Problem 3.
If a school kitchen has enough food for 234
pupils for 37 days, how long will the same food
last 73 pupils ?
Solution.
If you double, treble etc the number of pupils
what happens to the number of days ?
The days half, third etc.
This is inverse proportion.
What is the total number of pupil days ?
Pupil days 234 x37
8658 pupil days.
Divide the pupil days by the 73 pupils
8658 ? 73 118.6 days.
The kitchen can feed 73 pupils for 118 days at
most.
7
Problem 4.
You can exactly fit 7 volumes of an
encyclopaedia each 5.7cm thick on a shelf. How
many volumes each 6.7cm thick fit on the same
shelf ?
Solution
If you double , treble etc the thickness of the
encyclopaedia , what happens to the number of
volumes you can place on the shelf ?
Volumes half, third etc.
This is inverse proportion.
What is the total number of volume-centimetres ?
Volume-centimetres 7 x 5.7
39.9 volume centimetres
Divide the volume centimetres by the new volume
thickness .
39.9 ? 6.7 5.95 volumes.
You can place 5 volumes 6.7cm thick on the same
shelf.
8
What Goes In The Box?.
(1) If 7 electricians can wire some new houses in
17 days , how many electricians would be required
to do the job in 9 days ?
14 electricians.
(2) Jane can type at 6o words a minute and took
35minutes to complete a letter. How long would
John take who types at 43 words a minute ?
48.8 minutes.
(3) A car travelling at 45km/hr takes 33 minutes
for a journey. How long does a car travelling at
55km/hr take for the same journey ?
27 minutes.
9
The Cross- Multiplication Method.
We are going to apply the same method that we
used to solve direct proportion questions to
inverse proportion questions , with one
additional step to the process.
The method has the following strengths

• It is consistent with the method used for Direct
  Proportion.

• It establishes a strong and consistent routine
  for problem solving.

10
Consider the first problem again
Problem 1.
A farmer has enough cattle feed to feed 64 cows
for 2 days. How long would the same food last 32
cows ?
Solution
What two quantities are being talked about ?
Cattle
Days
What two numbers go together ?
64
2
Add in the additional information.
32
d
If you doubled, trebled etc the cattle, what
would happen to the number of days ?

Half, third etc.
Inverse proportion. Use arrows.
32d 2 x 64
Cross multiply to solve but flip over the second
column numbers to make it work.
d 128 ? 32 4 days.
11
Problem 2.
It takes 13 workers 27 hours to leaflet an area
of houses. How long would 22 workers take to do
the same work ?
Solution
What two quantities are being talked about ?
Workers
Hours
What two numbers go together ?
13
27
Add in the additional information.
22
h
If you doubled, trebled etc the workers, what
would happen to the number of hours ?

Half, third etc.
Inverse proportion. Use arrows.
32h 13 x 27
Cross multiply to solve but flip over the second
column numbers to make it work.
h 351 ? 32 7.84
It would take at least 8 hours to the nearest
hour to complete the task.
12
Problem 3.
A car travelling at an average speed of 67km/hr
takes 14 hours to complete a journey. How long
would the same journey take at 42km/hr ?
Solution
What two quantities are being talked about ?
Speed
Time
What two numbers go together ?
67
14
Add in the additional information.
42
t
If you doubled, trebled etc the speed, what would
happen to the time ?

Half, third etc.
Inverse proportion. Use arrows.
42t 67 x 14
Cross multiply to solve but flip over the second
column numbers to make it work.
h 938 ? 42 22.33
It would take 22.4 hours to complete the journey
at 42km/hr .
13
What Goes In The Box ? 2
(1) 24 workers take 14 days to deliver census
forms to all houses in a city . How many workers
could do it in 20 days ?
17 workers.
(2) A farmer can feed 245 sheep for 50 days. How
many days can he feed 152 sheep for with the same
amount of food ?
80 days
(3) I can afford 23 bars of chocolate at 27p a
bar . How many bars at 19p can I buy with the
same money ?
32 bars.
14
Graphs of Inverse Proportion.
Consider once again the first problem we looked
at
A farmer has enough cattle feed to feed 64 cows
for 2 days.
Complete the table below for the same amount of
cattle feed
We are going to draw a graph of the table.
Choose your scale carefully and allow each access
to go at least up to 65.
Estimate the position of the points (2,64) (4,32)
etc as accurately as you can.
15
(No Transcript)
16
The graph is a typical inverse proportion graph
It shows us that as the number of cows increases
The number of days decreases
Obviously the reverse is also true that if we
decrease the number of cows we will increase the
number of days feed.
17
What Goes In The Box ? 3
160 markers take 3 hours to complete marking
their examination scripts.
(a) Complete the table below
6
12
24
48
96
(b) Draw a graph of the table.
18
(No Transcript)