Switches with Input Buffers (Cisco)

1
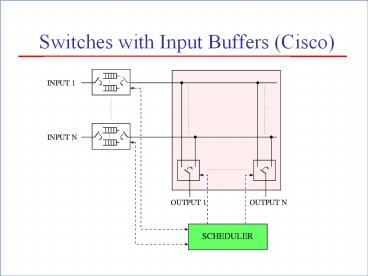
Switches with Input Buffers (Cisco)
2
Packet Switches with Input Buffers

• Switching fabric
• Electronic chips (Mindspeed, AMCC, Vitesse)
• Space-wavelength selector (NEC, Alcatel)
• Fast tunable lasers (Lucent)
• Waveguide arrays (Chiaro)
• Scheduler
• Packets compete not only with the packets
  destined for the same output but also with the
  packets sourced by the same input. Scheduling
  might become a bottleneck in a switch with
  hundreds of ports and gigabit line bit-rates.

3
Optical Packet Cross-bar (NEC,Alcatel)

• A 2.56 Tb/s multiwavelength and scalable
  switch-fabric for fast packet-switching network,
  PTL 1998,1999, NEC

4
Optical Packet Cross-bar (Lucent)

• A fast 100 channel wavelength tunable transmitter
  for optical packet switching, PTL 2001, Bell Labs

5
Scheduling Algorithms for Packet Switches with
Input Buffers

• Each input sends request for its HOL packet to
  the corresponding output. Each output grants one
  input, and this input-output pair will be
  connected in the next time slot.
• Output utilization when inputs are fully loaded
  is
• U1-(1-1/N)N-1

6
Scheduling Algorithms for Packet Switches with
Input Buffers
7
Scheduling Algorithms for Packet Switches with
Input Buffers

• In parallel iterative matching (PIM), SLIP or
  dual round-robin (DRR) inputs send requests to
  outputs, outputs grant inputs, and inputs then
  grant outputs in one iteration. It was proven
  that PIM finds a maximal matching after log2N
  4/3 steps on average.
• Maximum weighted matching and maximum matching
  algorithm maximize the weight of the connected
  pairs, and achieve 100 for i.i.d. traffic but
  have complexities O(N3log2N) and O(N2.5).
• Sequential greedy scheduling is a maximal
  matching algorithm that is simple to implement.
  Maximal matching algorithm does not leave
  input-output pair unmatched.

8
Bandwidth ReservationsPacket Switches with Input
Buffers

• Anderson et al. Time is divided into frames of F
  time slots. Schedule is calculated in each frame
  Statistical matching algorithm.
• Stiliadis and Varma Counters are loaded per
  frame. Queues with positive counters are served
  with priority according to parallel iterative
  matching (PIM), their counters are then
  decremented by 1. DRR proposed by Chao et al.
  could be used as well.
• Kam et al. Counter is incremented for the
  negotiated bandwidth and decremented by 1 when
  the queue is served. Maximal weighted matching
  algorithm is applied.
• Smiljanic Counters are loaded per frame. Queues
  with positive counters are served with priority
  according to the maximal matching algorithm
  preferrably sequential greedy scheduling
  algorithm (SGS), where inputs sequentially choose
  outputs to transmit packets to.

9
Maximum and Maximal Matching Algorithm

• It was shown that when packet arrivals are i.i.d
  and traffic distribution is admissible then 100
  can pass the cross-bar if the maximum or the
  maximum weighted matching algorithms are applied.
  
• It was shown that when packet arrivals obey a
  strong law of large numbers and traffic
  distribution is admissible then 50 can pass the
  cross-bar if the mximal matching algorithms are
  applied.

10
PIM, SLIP and DRR

• In PIM and SLIP each input sends requests to all
  outputs for which it has packets, and in DRR only
  to one chosen output. SLIP and DRR use
  round-robin choices.
• Theorem PIM finds a maximal matching after log2N
  4/3 steps on average.
• Proof Let n inputs request output Q, and let k
  of these inputs receive no grants. With
  probability k/n all requests are resolved, and
  with probability 1-k/n at most k requests are
  unresolved. The average number of requests is at
  most (1-k/n)kn/4. So if there are N2 requests
  at the beginning, the expected number of
  unresolved requests after I iterations is N2/4i

11
PIM, SLIP and DRR

• Proof (cont.) Let C be the last step on which
  the last request is resolved. Then

12
Typical Central Controllers (Cisco)
13
SGS Implementation

• All inputs one after another choose outputs, SGS
  is a maximal matching algorithm

14
SGS Uses Pipelining
Ii -gt Tk Input i chooses output for time slot k
15
Weighted Sequential Greedy Scheduling

• i1
• Input i chooses output j from Ok for which
  it has packet to send
  Remove i from Ik and j
  from Ok
• If iltN choose ii1 and
  go to the previous step

16
Weighted Sequential Greedy Scheduling

• If k1 mod F then cijaij
  Ik1,...,N Ok1,...,N i1
  
• Input i chooses output j from Ok for which
  it has packet to send such that cijgt0
  Remove i from Ik and j from Ok cijcij-1
• If iltN choose ii1 and
  go to the previous step

17
Non-blocking Nature of WSGS

• Maximal matching algorithm does not leave input
  or output unmatched if there is a packet to be
  transmitted from the input to the output in
  question.
• It can be proven that all the traffic passes
  through the cross-bar with the speedup of two
  which is run by a maximal matching algorithm, as
  long as the outputs are not overloaded.

18
Performance of Maximal Matching Algorithm
Theorem The maximal matching protocol (and so
WSGS) ensures aij time slots per frame to
input-output pair (i,j), if
where Ti is the number of slots reserved for
input i, and Rj is the number of slots reserved
for output j.
Proof Note that
19
Admission Control for Maximal Matching Algorithm
The maximal matching (and so WSGS) protocol
ensures aij time slots per frame to input-output
pair (i,j) if
F frame length Ti the number of slots reserved
for input i, Rj the number of slots reserved for
output j. ti, rj are normalized Ti, Rj.
20
Analogy with Circuit Switches

• Inputs Switches in the first stage
• Time slots in a frame Switches in the middle
  stage
• Outputs Switches in the last stage

Non-blocking condition
Strictly non-blocking condition
21
Rate and Delay Guranteed by Maximal Matching
Algorithm (and WSGS)

• Assume a coarse synchronization on a frame by
  frame basis, where a frame is the policing
  interval comprising F cell time slots of duration
  Tc.
• Then, the delay of D2FTc is provided for the
  utilization of 50. Or, this delay and
  utilization of 100 are provided for the fabric
  with the speedup of 2.

22
Port Congestion Due to Multicasting
Solution Packets should be forwarded through
the switch by multicast destination ports.
23
Forwarding Multicast Traffic
24
Forwarding Multicast Traffic
25
Forwarding Multicast Traffic
26
Adding the Port to the Multicast Tree
27
Removing the Port from the Multicast Tree
28
Admission Control for Modified WSGS
where Ei is the number of forwarded packets per
frame
29
Admission Control for Modified WSGS
for

30
Admission Control for Modified WSGS
Modified WSGS protocol ensures negotiated
bandwidths to input-output pairs if for

I
II

F frame length, P forwarding fan-out
Ti the number of slots reserved for input i, Ri
the number of slots reserved for output i. ti,
ri are normalized Ti, Ri.
31
Rate and Delay Guaranteed by Modified WSGS

• Assume again a coarse synchronization on a frame
  by frame basis.
• Then, the delay of D FTc is
  provided for the utilization of 1/(P2), where P
  is the forwarding fan-out. Or, this delay and
  utilization of 100 are provided for the fabric
  speedup of P2.

32
Quality of Service, P2, S4, B10Gb/s, Tc50ns
N 1000 1000 4000 4000
F 104 5104 104 5104
C Tb/s 2.5 2.5 10 10
G Mb/s 1 0.2 1 0.2
D ms 5 25 5.5 27.5
33
References

• T. E. Anderson, S. S. Owicki, J. B. Saxe, and C.
  P. Thacker, Highspeed switch scheduling for
  local-area networks, ACM Transactions on
  Computer Systems, vol. 11, no. 4, November 1993,
  pp. 319-352.
• N. McKeown et al., The Tiny Tera A packet
  switch core, IEEE Micro, vol. 17, no. 1,
  Jan.-Feb. 1997, pp. 26-33.
• A. Smiljanic, Flexible bandwidth allocation in
  high-capacity packet switches, IEEE/ACM
  Transactions on Networking, April 2002, pp.
  287-293.

34
References

• A. Smiljanic, Scheduling of multicast trafc in
  high-capacity packet switches, IEEE
  Communication Magazine, November 2002, pp. 72-77.