6. Radial-basis function (RBF) networks

1
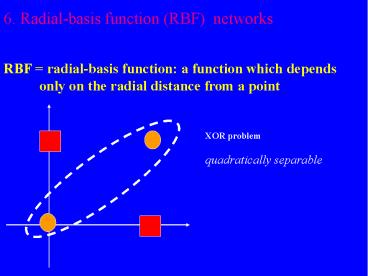
6. Radial-basis function (RBF) networks RBF
radial-basis function a function which depends
only on the radial distance from a
point
XOR problem quadratically separable
2
So RBFs are functions taking the
form Where f is a nonlinear activation
function, x is the input and xi is the ith
position, prototype, basis or centre vector. The
idea is that points near the centres will have
similar outputs I.e. if x xi then f (x) f
(xi) since they should have similar properties.
Therefore instead of looking at the data points
themselves characterise the data by their
distances from the prototype vectors (similar to
kernel density estimation)

3
For example, the simplest form of f is the
identity function f (x) x
x1(0,1)
x d1 d2 (0,0)
1 1.1 (1,1) 1 .5 (0,1)
0 1.1 (1,0) .5
x2(1,0.5)
Now use the distances as the inputs to a network
and form a weighted sum of these
4
Can be viewed as a Two-layer network
y1
y2
Input
Output
d
wj
yM
fN (y)f y-xN
Hidden layer
output S wi fi(y) adjustable parameters are
weights wj number of hidden units number of
prototype vectors Form of the basis functions
decided in advance
5

• use a weighted sum of the outputs from the basis
  functions for e.g. classification, density
  estimation etc
• Theory can be motivated by many things
  (regularisation, Bayesian classification, kernel
  density estimation, noisy interpolation etc), but
  all suggest that basis functions are set so as to
  represent the data.
• Thus centres can be thought of as prototypes of
  input data.

1
0


0
O1
MLP vs RBF distributed local
6
E.g. Bayesian interpretation if we choose to
model the probability and we choose appropriate
weights then we can interpret the outputs as the
posterior probabilities Ok P(Ck(x) a p(xCk)
P(Ck)
O1
O2
O3
0
0
P(C1)
P(C3)
F1(x) p(xC1)
F3(x) p(xC3)
x
y
7
Starting point exact interpolation Each input
pattern x must be mapped onto a target value d
d
x
8
That is, given a set of N vectors xi and a
corresponding set of N real numbers, di (the
targets), find a function F that satisfies the
interpolation condition F ( xi ) di for
i 1,...,N or more exactly find
satisfying
9
Example XOR problem
x d (0,0)
0 (1,1) 0 (0,1)
1 (1,0) 1
Exact interpolation RBF placed at position of
each pattern vector using 1) linear RBF
10
i.e. 4 hidden units in network
Network structure
11
w1 w2 w3 w4
0 1 1 1 0 1
1 0 1 1 1 0
0 1 1 0

w1 w2 w3 w4
1 1
Results

12
And general solution is
Ie F(x1,x2) sqrt(x12x22)
sqrt((x1-1)2x22)
sqrt(x12(x2-1)2)
sqrt((x1-1)2(x2-1)2)
13
For n vectors get
Interpolation Matrix
weight
f ( x i - xj ) scalar function of distance
between vector x i and xj
Equivalently
F W D
14
If F is invertible we have a unique solution of
the above equation Micchellis Theorem Let xi
, i 1, ..., N be a set of distinct points in
Rd, Then the N-by-N interpolation matrix , whose
ji-th element is f ( x i - xj ) , is
nonsingular.
So provided F is nonsingular then interpolation
matrix will have an inverse and weights to
achieve exact interpolation
15
Easy to see that there is always a solution. For
instance, if we take f(x-y)1 if x y, and 0
otherwise (e.g. a Gaussian with very small s),
setting widi solves the interpolation
problem However, this is a bit trivial as the
only general conclusion about the input space is
that the training data points are different.
16

• To summarize
• For a given data set containing N points
  (xi,di), i1,,N
• Choose a RBF function f
• Calculate f(xj - xi )
• Obtain the matrix F
• Solve the linear equation F W D
• Get the unique solution
• Done!

Like MLPs, RBFNs can be shown to be able to
approximate any function to arbitrary accuracy
(using an arbitrarily large numbers of basis
functions). Unlike MLPs, however, they have
the property of best approximation i.e. that
there exists an RBFN with minimum approximation
error.
17
Other types of RBFs include

• Multiquadrics
• for some cgt0
• (b) Inverse multiquadrics
• for some cgt0
• Gaussian
• for some s gt0

18
Linear activation function has some undesirable
properties e.g. f (xi) 0. (NB f is still a
non-linear function as it is only piecewise
linear in x).

• Inverse multiquadrics and Gaussian RBFs are both
  examples
• of localized functions
• Multiquadrics RBFs are nonlocalized functions

19
Localized as distance from the centre
increases the output of the RBF decreases
20

• Nonlocalized as distance from the centre
  increases the output of the RBF increases

21
Example XOR problem
x d (0,0)
0 (1,1) 0 (0,1)
1 (1,0) 1
Exact interpolation RBF placed at position of
each pattern vector using 2) Gaussian RBF with s1
22
i.e. 4 hidden units in network
Network structure
23
w1 w2 w3 w4
exp(0) exp(-.5) exp(-.5) exp(-1) exp(-.5)
exp(0) exp(-1) exp(-.5) exp(-.5) exp(-1)
exp(0) exp(-.5) exp(-1) exp(-.5)
exp(-.5) exp(0)
0 1 1 0

w1 w2 w3 w4
-3.0359 3.4233 3.4233 -3.0359
Results

24
1) f(x1,x2) sqrt(x12x22) -
sqrt((x1-1)2x22) -
sqrt(x12(x2-1)2)
sqrt((x1-1)2(x2-1)2)
2) f(x1,x2) -3.0359 exp(-(x12x22)/2)
3.4233 exp(-(x1-1)2x22)/2)
3.4233 exp(-(x12(x2-1)2)/2)
-3.0359 exp(-(x1-1)2(x2-1)2)/2)
25
Large s 1
26
Small s 0.2
27
Problems with exact interpolation can produce
poor generalisation performance as only data
points constrain mapping overfitting
problem Bishop(1995) example Underlying
function f(x)0.50.4sine(2pi x) sampled randomly
for 30 points added gaussian noise to each data
point 30 data points 30 hidden RBF
units fits all data points but creates
oscillations due added noise and unconstrained
between data points
28
All Data Points
5 Basis functions
29

• To fit an rbf to every data point is very
  inefficient due to the computational cost of
  matrix inversion and is very bad for
  generalisation so
• Use less RBFs than data points I.e. MltN
• Therefore dont necessarily have RBFs centred at
  data points
• Can include bias terms
• Can have gaussians with general covariance
  matrices but there is a trade-off between
  complexity and the number of parameters to be
  found

30
1 parameter
d parameters
for d rbfs we have
d(d1)/2 parameters
31
6. Radial-basis function (RBF) networks
II Generalised radial basis function
networks Exact interpolation expensive due to
cost of matrix inversion prefer fewer centres
(hidden RBF units) centres not necessarily at
data points can include biases can have
general covariance matrices now no longer exact
interpolation, so where M (number of hidden
units) ltN (number of training data)
32
Three-layer networks
f0 1
x1
x2
w0 bias
Input nD vector
Output
y
wM
fM (x)f (x-xM)
xN
Hidden layer

1. output S wi fi(x)
2. adjustable parameters are weights wj, number of
   hidden units M (ltN)
3. Form of the basis functions decided in advance

33
F(x)
F(x)
S
S
w1
w2
w31
w32
sig(w1Tx)
f(r1)
f(r2)
sig(w2Tx)

w1
w2
r2

x
x
r1
w1Tx k
34
Comparison of MLP to RBFN MLP hidden unit
outputs are monotonic functions of a weighted
linear sum of the inputs gt constant on (d-1)D
hyperplanes distributed representation as many
hidden units contribute to network output gt
interference between units gt non-linear training
gt slow convergence
RBF hidden unit outputs are functions of
distance from prototype vector (centre) gt
constant on concentric (d-1)D hyperellipsoids lo
calised hidden units mean that few contribute to
output gt lack of interference gt faster
convergence
35
Comparison of MLP to RBFN MLP more than one
hidden layer global supervised learning of all
weights global approximations to nonlinear
mappings
RBF one hidden layer hybrid learning with
supervised learning in one set of
weights localised approximations to nonlinear
mappings
36
Three-layer networks
f0 1
x1
x2
w0 bias
Input nD vector
Output
y
wM
fM (x)f (x-xM)
xN
Hidden layer

1. output S wi fi(x)
2. adjustable parameters are weights wj, number of
   hidden units M (ltN)
3. Form of the basis functions decided in advance

37
Hybrid training of RBFN Two stage hybrid
learning process stage 1 parameterise hidden
layer of RBFs - hidden unit number (M)
-centre/position (ti) -width
(s) use unsupervised methods (see below) as they
are quick and unlabelled data is plentiful. Idea
is to estimate the density of the data stage 2
Find weight values between hidden and output
units minimize sum-of-squares error between
actual output and desired responses --invert
matrix F if MN --Pseudoinverse of F if
MltN Stage 2 later, now concentrate on stage 1.
38
Random subset approach Randomly select centres
of M RBF hidden units from N data points widths
of RBFs usually common and fixed to ensure a
degree of overlap but based on an average or
maximum distance between RBFs e.g. s
dmax /sqrt (2M) where dmax is the maximum
distance between the set of M RBF units The
method is efficient and fast, but suboptimal and
its important to get s correct
39
s 10
s 0.08
s 0.4
40
Clustering Methods K-means algorithm --divides
data points into K subgroups based on
similarity Batch version 1. Randomly assign
each pattern vector x to one of K subsets 2.
Compute mean vector of each subset 3. Reassign
each point to subset with closest mean vector
4. Until no further reassignments, loop back to
2 On-line version 1. Randomly choose K data
points to be basis centres mi 2. As each vector
is xn presented, update the nearest mi using
?mi h(xn - mi) 3. Repeat until no further
changes
41
The covariance matrices (s) can now be set to the
covariance of the data points of each subset --
However, note that K must be decided at the
start -- Also, the algorithm can be sensitive to
initial conditions -- Can get problems of no/few
points being in a set see competitive learning
lecture -- Might not cover the space
accurately Other unsupervised techniques such as
self organising maps and Gaussian mixture models
can also be used Another approach is to use
supervised techniques where the parameters of the
basis functions are adaptive and can be
optimised. However, this negates the speed and
simplicity advantages of the 1st stage of
training.
42
Relationship with probability density function
estimation
Radial basis functions can be related to kernel
density functions (Parzen windows) used to
estimate probability density functions E.g. In 2
dimensions the pdf at a point x can be estimated
from the fraction of training points which fall
within a square of side h centred on x
Here p(x) 1/6 x 1/(hxh) x Sn H(x-xn,h) where H
1 if xn-x lt h ie estimate density by fraction
of points within each square Alternatively,
H(xn-x) could be gaussian giving a smoother
estimate for the pdf
43
In Radial basis networks the first stage of
training is an attempt to model the density of
the data in an unsupervised way As in kernel
density estimation, we try to get an idea of the
underlying density by picking some prototypical
points Then use distribution of the data to
approximate a prior distribution
44
Back to Stage 2 for a network with M lt N basis
vectors
Now for each training data vector ti and
corresponding target di we want F ( ti ) di ,
that is, we must find a function F that
satisfies the interpolation condition F (
ti ) di for i 1,...,N Or more exactly
find satisfying
45
So the interpolation matrix becomes
Which can be written as F W D where F
is an MxN matrix (not square).
46
To solve this we need to generate an error
function such as the least squares error
and minimise it. As the derivative of the least
squares error is a linear function of the weights
it can be solved using linear matrix inversion
techniques (usually singular value decomposition
(Press et al., Numerical Recipes)). Other error
functions can be used but minimising the error
then becomes a non-linear optimisation problem.
47
However, note that the problem is
OverDetermined That is, by using N training
vectors and only M centres we have M unknowns
(the weights) and N bits of information eg
training vectors (-2, 0), (1, 0), targets 1, 2
centre (0, 0), linear rbf F W D gt
w 0.5 or w 2 ??? Unless NM and there are no
degeneracies (parallel or nearly parallel) data
vectors, we cannot simply invert the matrix and
must use the pseudoinverse (using Singular Value
Decomposition).
48
Alternatively, can view this as an ill-posed
problem Ill-posed problems (Tikhonov) How do we
infer function F which maps X onto y from a
finite data set? This can be done if problem is
well-posed - existence each input
pattern has an output - uniqueness each
input pattern maps onto only one output -
continuity small changes in input pattern
space imply small changes in y
In RBFs however - noise can violate continuity
condition - different output values for same
input patterns violates uniqueness -
insufficient information in training data may
violate existence condition
49
Ill-posed problem the finite data set does not
yield a unique solution
50

• Regularization theory (Tikhonov, 1963)
• To solve ill-posed problems need to supplement
  finite data set
• with prior knowledge about nature of mapping
  
• -- regularization theory
• common to place constraint that mapping is
  smooth (since smoothness implies continuity)
• add penalty term to standard sum-of squares
  error for non-smooth mappings
• E(F)ES (F) l Ec(F)
• where eg
• ES (F) 1/2 S ( di- F(xi) )2 and
  Ec(F)1/2 DF 2
• and DF could be, say the first or second order
  derivative of F etc.

51

• l is called the regularization parameter
• l 0 unconstrained (smoothness not
  enforced)
• l infinity, smoothness constraint
  dominates and less
• account is taken
  of training data error
• l controls balance (trade-off) between a
  smooth mapping and fitting the data points exactly

52
EC curvature
l 0
l 40
53
Regularization networks --Poggio Girosi (1990)
applied regularization theory to RBF
networks --By minimizing the new error function
E(F) we obtain (using results from
functional analysis) where I is the unit
matrix. Provided EC is chosen to be quadratic in
y, this equation can be solved using the same
techniques as the non-regularised network.
54
Problems of RBFs
1. Need to choose number of basis functions 2.
Due to local nature of basis functions has
problems in ignoring noisy input dimensions
unlike MLPs (helps to use dimensionality
reduction such as PCA)
1D data, M rbfs
Same data with uncorrelated noise, M2 rbfs
55
Problems of RBFs 2
3. Optimal choice of basis function parameters
may not be optimal for the output task
Data from h gt rbf at a, but gives a bad
representation of h. In contrast, one centred at
b would be perfect
56
Problems of RBFs 3
4. Because of dependence on distance, if
variation in one parameter is small with respect
to the others it will contribute very little to
the outcome (l e)2 l2. Therefore, preprocess
data to give zero mean and unit variance via
simple transformation x (x - m) s
(Could achieve the same using general covariance
matrices but this is simpler)
57
However, this does not take into account
correlations in the data.
Better to use whitening (Bishop, 1995, pp
299-300)
58
x L-1/2 UT (x - m) where U is a matrix
whose columns are the eigenvectors ui of S, the
covariance matrix of the data, and L a matrix
with the corresponding eigenvalues li on the
diagonals i.e U (u1, , un) And
L diag(l1, , ln)
l1u1
l2u2
59
Using RBF Nets in practice

• Choose a functional form (Gaussian generally,
  but prior knowledge/experience may suggest
  others)
• Select the type of pre-processing
• --Reduce dimensionality (techniques to follow in
  next few lectures) ?
• --Normalise (whiten) data?
• (no way of knowing if these will be helpful may
  need to try a few combinations)
• Select clustering method (k-means)
• Select number of basis functions, cluster and
  find basis centres
• Find weights (via matrix inversion)
• Calculate performance measure.

60
If only life were so simple

• How do we choose k? Similar to problem of
  selecting number of hidden nodes for MLP
• What type of pre-processing is best?
• Does the clustering method work for the data?
  E.g might be better to fix s and try again.
• There is NO general answer each choice will be
  problem-specific. The only info you have is your
  performance measure.

61
Idea try e.g. increasing k until performance
measure decreases (or gets to a minimum, or
something more adventurous).
Performance measure
Optimal k?
k
Note the dependence on the performance measure
(make sure its a good one). Good thing about RBF
Nets is that the training procedure is relatively
quick and so lots of combinations can be used.