Shear Sort

1
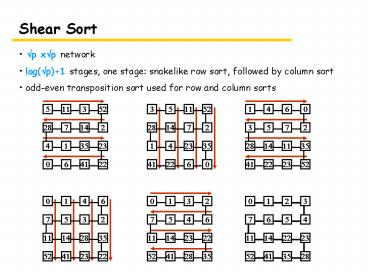
Shear Sort

• ?p x?p network
• log(?p)1 stages, one stage snakelike row sort,
  followed by column sort
• odd-even transposition sort used for row and
  column sorts

2
Shear Sort in r x s network

• how to distribute the data?
• how to do snakelike order? horizontal? vertical?
• how many stages are needed?
• what is the cost of each stage?
• what is the total cost?
• which choice is the best?

3
Bitonic Sort
BM2s
BM4s
BM8s
10
10
5
3
20
20
9
5
5
9
10
8
9
5
20
9
3
3
14
10
8
8
12
12
12
14
8
14
14
12
3
20
90
0
0
95
0
90
40
90
60
60
60
60
40
40
90
40
23
23
95
35
35
35
35
23
95
95
23
18
18
18
18
0
4
Bitonic Sort High Level Code
void BitSort(int myId, int p, double myData)
int i, j sort(myData, )
for(i0 iltlog(p) i) for(ji jgt0 j--)
if (myId 2j) dest myId - 2j
else dest myId 2j if (myId
2i1) dir DOWN else
dir UP CompareSwap(myId,
dest, myData, dir)
5
Bitonic Sort VIII
Mapping Bitonic Sort to a Hypercube (n
processors)
0000
1
0001
2,1
0010
1
0011
3,2,1,
0100
1
0101
2,1
0110
1
0111
4,3,2,1,
1000
1
1001
2,1
1010
1
1011
3,2,1
1100
1
1101
2,1
1110
1
1111
6
Bitonic Sort IX
BM16 in hypercube in detail
7
Bitonic Sort X
Overall complexity in a hypercube n processors
Tp O(log2 n) O(log2 n)
comparisons communication

• p processors
• n/p comparators per process
• use compare-and-swap operations

Tp O(n/p log(n/p)) O(n/p log2 p) O(n/p
log2 p)
local sort comparisons
communication
8
Bitonic Sort XI
BM16 in mesh in detail
step 1 dim 4
0000
0001
0010
0011
Normal mapping
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
step 2 dim 3
step 3 dim 2
step 4 dim 1
9
Costs

• Step 1 and Step 3 run at half speed, because of
  congestion
• Overall cost of BitonicSort16 is
  BM2BM4BM8BM16
• Step 1 would be used only once in BM16
• Step 2 would be used twice (in BM16 and BM8)
• Step 3 3 times
• Step 4 4 times
• Overall cost 4 times slow steps 6 times fast
  steps 14 fast steps
• In general, consider step log(n)/2. It is
  executed log(n)/2 times, and congestion is O(?
  n), making the total communication at least
  O(log(n)?n).
• Can we do better?

10
Bitonic Sort in Mesh Better Mapping
Idea reorganize the nodes so that the most
common steps are the cheapest.
11
Bitonic Sort XII
Overall complexity in a mesh n processors Tp
O(log2 n) O(?n)
comparisons communication, with smart
embedding

• p processors
• n/p comparators per process
• use compare-and-swap operations

Tp O(n/p log(n/p)) O(n/p log2 p) O(n/?p)
local sort comparisons
communication
12
Parallel Quicksort

• Sequential Quicksort
• choose pivot
• split the sequence into L (ltpivot) and R (gt
  pivot)
• recursively sort L and R
• Naïve Parallel Quicksort
• parallelise only the last step
• Complexity
• O(nn/2n/4) O(n) (average)
• dominated by the sequential splitting
• only log n processors can be efficiently used

13
Parallel Quicksort II

• Parallel Quicksort for shared memory computer
• every processor gets n/p elements
• repeat
• choose pivot and broadcast it
• each processor i splits its sequence into Li
  (ltpivot) and Ri (gt pivot)
• collect all Lis and Ris into global L and R
• split the processors into left and right in the
  ratio L/R
• the left processors recursively sort L, the
  right processors R
• until a single processor is left for the whole
  (reduced) range
• sort your range sequentially

14
Parallel Quicksort III
15
Parallel Quicksort IV
16
Parallel Quicksort V
17
Parallel Quicksort VI
18
Parallel Quicksort VII

• Complexity analysis
• selecting pivot O(1)
• broadcasting pivot O(log p)
• local rearrangement O(n/p)
• global rearrangement O(log p n/p)
• multiply by log p iterations
• local sequential sort O(n/p log (n/p))
• Overall complexity
• O(n/p log n/p) O(n/p log p) O(log2 p)

lDest Scan( Li, , )
rDest Scan( Ri, , ) copyElements(AlDest,
Li , Li,) copyElements(AlSizerDest, Ri ,
Ri,)
local sort local rearr.
broadcasting and scan()
global moving
19
Parallel Quicksort VIII

• Message passing implementation
• more complications with explicit moving the data
  around
• main complication in the global rearrangement
  phase
• each process may need to send its Li and Ri to
  several other processes
• each process may receive its new Li and Ri from
  several other processes
• the destination of the pieces of Li and Ri
  (where to send them in the global rearrangement)
  contains destination process and an address
  within that process
• all-to-all communication may be necessary
• asymptotic complexity remains the same
• Importance of pivot selection

20
Bucket Sort

• Assumptions
• data uniformly distributed in an interval a,b
• each processors starts with n/p elements (block
  partitioning)
• High-level description
• logically divide the interval a,b into p
  equal-sized sub-intervals Ii
• distribute the local data into p buckets an
  element from interval Ii goes to bucket Bi (each
  processors has p local buckets)
• collect the contents of the buckets into
  appropriate processors (i.e. each processor sends
  the contents of its local bucket Bi to pi
• sequentially sort the received data (your
  bucket)
• Complexity (assuming uniform distribution)
• O(n/p log(n/p) communication)

21
Sample Sort

• Goal get rid of the uniformly distributed data
  assumption
• Idea sample the input data and compute a good
  set of bucket intervals
• High-level description
• sort local data and choose p-1 evenly spaced
  pivots
• send these pivots to the master process
• master collects all p(p-1) pivots, sorts them
  and chooses p-1 evenly spaced (among the p(p-1)
  pivots) master pivots
• master broadcasts the master pivots
• the master pivots define the buckets used by
  each process
• continue as in the bucket sort
• distribute local data into the buckets (e.g by
  inserting the master pivots using binary search
  into the sorted local sequence)
• send buckets to appropriate processes
• sort the received data

22
Sample Sort Complexity

• Lemma Each processor will receive at most 2n/p
  elements.
• Idea sample the input data and compute a good
  set of bucket intervals
• Parallel Time
• sort local data O(n/p log (n/p))
• and choose p-1 evenly spaced pivots O(p)
• send these pivots to the master process O(p2)
• master sorting all pivots O(p2 log p)
• selecting master pivots O(p)
• broadcasting master pivots O(p log p)
• dividing into local buckets O(p log n/p)
• all2all of the contents of the local buckets
  depends, O(nplog p)
• final sort O(n/p log (n/p))

23
Sample Sort Complexity II
Parallel Time (assuming roughly uniform
distribution) Tp Q(n/p log(n/p)) Q(p2 log p)
Q(p log n/p) Q(n/pp log p)
local sort sort pivots partitioning
communication

• Note
• bitonic sort may be used to sort the pivots
• could reduce the time to sort pivots to O(p log2
  p)
• how to select and broadcast master pivots when
  the sorted pivots are distributed?
• makes sense only if the sorting of pivots is the
  costliest part

24
Sorting Conclusions
Odd-even transposition sort O(n) time with n
processors, for linear array, simple,
inefficient, the best we can hope for in linear
array if only communication with direct
neighbours is possible Shear sort O(?n (log n
1)) time with n processors, for 2D mesh, simple,
there is an O(?n) version, which is optimal in 2D
mesh if only communication with direct neighbours
is possible Bitonic sort O(log2 n) time with n
processors (in hypercube), simple, still not cost
optimal, hypercube and 2D mesh implementations Qui
ck Sort O(log2 n) time with n processors (with
good pivots), shared memory and message-passing
implementations Sample Sort for ngtp2, alleviates
partially the problem of uneven data
distribution There exists O(log n) sorting
algorithm with n processors, but it is very
complicated and the constant factors are too high
to be practical.