Lattice Theory - PowerPoint PPT Presentation
1 / 32
Title:
Lattice Theory
Description:
Lattice Theory Symmetry not involving translation yields symmetry about a point, i.e., the 32 point groups Translation is the periodic repeat in 1, 2, or 3 directions – PowerPoint PPT presentation
Number of Views:1490
Avg rating:3.0/5.0
Title: Lattice Theory
1
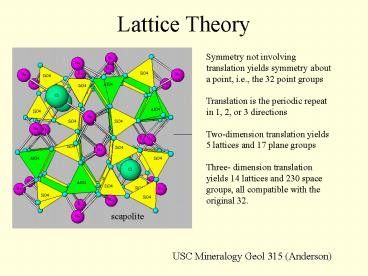
Lattice Theory
Symmetry not involving translation yields
symmetry about a point, i.e., the 32 point
groups Translation is the periodic repeat in 1,
2, or 3 directions Two-dimension translation
yields 5 lattices and 17 plane groups Three-
dimension translation yields 14 lattices and 230
space groups, all compatible with the original
32.
scapolite
USC Mineralogy Geol 315 (Anderson)
2
Lattice Theory
We are surrounded by patterns and symmetry
translation
reflection
rotation
3
Lattice Theory
translation
Unit cell the smallest space that upon
translation fills all space
Reflection with translation
4
Lattice Theory
screw axis
Translation with rotation
Translation with rotation
5
Lattice Theory
Screw Axis - Rotation Translation
Quartz - the spiral of silica tetrahedrons // c
6
2-D Lattice Theory
Symmetry elements include most of those seen in
point groups including rotation (2, 3, 4, 6) and
reflection (m), but also simple translation and
glide (reflection plus translation)
rotation
reflection
translation
glide
7
Five Plane Lattices
Parallelogram (clinonet) x ? y, ? ?
90 Rectangle (orthonet) x ? y, ?
90 Rhombic (centered orthonet) same
with center Hexanet xy, ? 60 Square
or Tetranet xy, ? 90
8
Five Plane Lattices
9
Plane Group p1
Simple and common in patterns - only translation
in a parallelogram unit cell
Images from http//www.clarku.edu/djoyce/wallpape
r/lattices.html
10
Plane Group p2
P primitive (not centered) unit cell
Translation plus 2-fold rotation in a
parallelogram unit cell
11
Plane Group pm
Translation plus reflection in a parallelogram
unit cell
12
(No Transcript)
13
Plane Group pg
Primitive lattice with a glide
14
(No Transcript)
15
Point Group pg
the pattern
unit cells
symmetry
16
(No Transcript)
17
Plane Group cm
Centered unit cell with mirrors (red) and glides
(green)
18
(No Transcript)
19
Plane group pmm
Primitive rectangular lattice with orthogonal
mirrors (red) and 2-fold rotation (dots)
20
Plane Group pmg
Primitive lattice with glides, mirrors, and
2-fold rotation
21
(No Transcript)
22
Plane group pgg
Primitive rectangular lattice with orthogonal
glides (green)
23
Plane Group cmm
Centered cell (rhombic) with orthogonal mirrors
(and glides)
24
(No Transcript)
25
Plane Group p4
Primative square net with 4-fold and 2-fold
rotation
26
Plane group p4m
Square net with rotations (4, 2) plus reflection
27
(No Transcript)
28
Plane Group p4g
Primitive square net with rotation (4, 2) and
orthogonal mirrors and glides
29
Plane group p3
Primitive hexanet with only 3-fold rotation
30
Final four plane groups
p13m
p3m1
p6m
p6
31
Minerals and Symmetry
gypsum
Minerals exhibit symmetry in all of their
dimensions, from their external form (point) to
two (plane) and three dimensions (space).
32
Mineral of the Day
halite