Why does a circle have 360

1
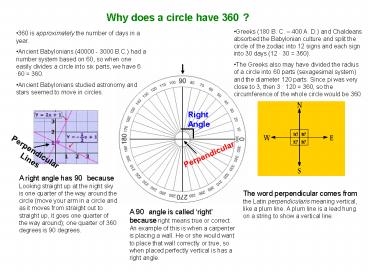
Why does a circle have 360?

• Greeks (180 B. C. 400 A. D.) and Chaldeans
  absorbed the Babylonian culture and split the
  circle of the zodiac into 12 signs and each sign
  into 30 days (12 30 360).
• The Greeks also may have divided the radius of a
  circle into 60 parts (sexagesimal system) and the
  diameter 120 parts. Since pi was very close to 3,
  then 3 120 360, so the circumference of the
  whole circle would be 360.

• 360 is approximately the number of days in a
  year.
• Ancient Babylonians (40000 - 3000 B.C.) had a
  number system based on 60, so when one easily
  divides a circle into six parts, we have 6 60
  360.
• Ancient Babylonians studied astronomy and stars
  seemed to move in circles.

Right Angle
Perpendicular Lines
Perpendicular
A right angle has 90 because Looking straight up
at the night sky is one quarter of the way around
the circle (move your arm in a circle and as it
moves from straight out to straight up, it goes
one quarter of the way around) one quarter of
360 degrees is 90 degrees.
The word perpendicular comes from the Latin
perpendicularis meaning vertical, like a plum
line. A plum line is a lead hung on a string to
show a vertical line.
A 90 angle is called right because right means
true or correct. An example of this is when a
carpenter is placing a wall. He or she would want
to place that wall correctly or true, so when
placed perfectly vertical is has a right angle.
2

• Jennifer Cornish
• History of Math Poster
• July 17, 2008
• NCTM Historical Topics for the Mathematics
  Classroom. 1969.pp. 362-365.
• Smith. History of Mathematics, Volume II. 1953.p.
  232.
• http//www.auburn.edu/communications_marketing/ask
  aubie/032305.html
• http//www.etymonline.com/index.php?searchperpend
  icularsearchmodenone