Thermal Equilibrium

1
Thermal Equilibrium
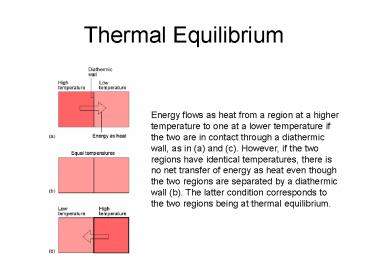
Energy flows as heat from a region at a higher
temperature to one at a lower temperature if the
two are in contact through a diathermic wall, as
in (a) and (c). However, if the two regions have
identical temperatures, there is no net transfer
of energy as heat even though the two regions are
separated by a diathermic wall (b). The latter
condition corresponds to the two regions being at
thermal equilibrium.
2
Zeroth Law of Thermodynamics
The experience summarized by the Zeroth Law of
thermodynamics is that, if an object A is in
thermal equilibrium with B and if B is in
thermal equilibrium with C, then B is in thermal
equilibrium with A.
3
Mechanical Equilibrium
When a region of high pressure is separated from
a region of low pressure by a movable wall, the
wall will be pushed into one region or the other,
as in (a) and (c). However, if the two pressures
are identical, the wall will not move (b). The
latter condition is one of mechanical equilibrium
between the two regions.
4
Measurement of Pressure
Two versions of a manometer used to measure the
pressure of a sample of gas. (a) The height
difference, h, of the two columns in the
sealed-tube manometer is directly proportional to
the pressure of the sample, and p rgh, where r
is the density of the liquid. (b) The difference
in heights of the columns in the open-tube
manometer is proportional to the difference in
pressure between the sample and the atmosphere.
In the example shown, the pressure of the sample
is lower than that of the atmosphere.
5
Important Gases in Biology

• O2 carried by red blood cells
• for aerobic respiration
• Partial pressure of oxygen from Krogh cylinder
  model
• C02 waste product
• NO nitrous oxide
• Released by endothelial cells, Affects vascular
  tone

6
Boyles Law(valid at low pressures)
The pressure-volume dependence of a fixed amount
of perfect gas at different temperatures. Each
curve is a hyperbola (pV constant) and is
called an isotherm.
7
Charles Law
The variation of the volume of a fixed amount of
gas with the temperature constant. Note that in
each case they extrapolate to zero volume at
-273.15? C. The lines are isotherms.
8
Ideal Gas Law

• Combine Charles and Boyles Laws with Avogardos
  Principle (equal volumes of gases at same T, P
  have same number of molecules)
• ? PV nRT
• A thermodynamic equation of state

9
Three Dimensional Surfaces
10
Daltons Law of Partial Pressure
Pressure exerted by mixed gas is sum of the
partial pressures p pApB Recall mole
fraction xJnJ/n n nAnB Partial
pressure pJ xJp
11
Intermolecular Forces

• Affect real gases

The variation of the potential energy of two
molecules on their separation. High positive
potential energy (at very small separations)
indicates that the interactions between them are
strongly repulsive at these distances. At
intermediate separations, where the potential
energy is negative, the attractive interactions
dominate. At large separations (on the right) the
potential energy is zero and there is no
interaction between the molecules.
12
Real Gases

• Due to intermolecular forces, the Ideal gas law
  breaks down
• Understanding deviations from ideal gas behavior
  teach us about molecular interactions
• Van der Waals Eqn and Virial Expansion
• Coefficients relate to energy of interaction
  between molecules

13
Compression Factor
Variation of Z with Pressure At 0 C
Low pressures, Z1, all gases ideal At high
pressures, Vreal gtVideal Zgt1 repulsive
forces dominate Low pressure, Vreal ltVideal, Zlt
1 attractive forces dominate Low temperatures -gt
molecules moving less rapidly more influenced by
attractive forces
14
Van der Waals Equation (1873)
a reflects how strongly molecules attract each
other b corrects for the molecules size
15
Derivation of vdw Eq. State

• Repulsive interactions cause molecules to behave
  as impenetrable spheres
• Molecules restricted to smaller volume V-nb,
  where nb is volume molecules take up
• Pressure depends on frequency of collisions with
  walls and force of each collision both reduced
  by attractive forces proportional to molar
  concentration (n/V)
• Pressure is then reduced according to a(n/V)2

16
Vdw surfaces
The oscillations are called van der Waals loops
and are unphysical suggest that increasing
pressure increases volume They occur below the
critical temperature
See Applets at http//www.whfreeman.com/pchem7/co
n_index.htm?01
17
Phase Transition Condensation
Imagine you are compressing gas with piston At C,
piston slides without further change in
pressure Liquid begins to appear Two phases
coexist Going to E amount of liquid
increases Pressure along CDE is vapour
pressure At E, sample is liquid now the
compressibility changes .
Similar behave happens in lipidic or polymeric
systems, which exhibit a rich variety of phase
transitions
Experimental isotherms of CO2 at several
temperatures.
18
Critical Constants
The critical isotherm', the isotherm at the
critical temperature Tc, is at 31.04 ?C. The
critical point is marked with a star. Critical
pressure Pc Critical molar volume Vc Tc, Pc,Vc
critical constants If you compress along Tc,
liquid does not appear these highly dense
materials are called supercritical fluids and
their properties are a subject of intense current
research
19
Other Equations of State

• Redlich-Kwong Peng-Robinson
• Both are quantitative in region where gas
  liquefies
• Berthelot,Dieterici and others with more than ten
  parameters can give good fits !!!
• with seven free parameters, you can describe an
  elephant

20
Principle of Corresponding States

• All gases have the same properties if they are
  compared at corresponding conditions
• Define reduced variables
• For homework you will write the vdw eqn in terms
  of the reduced variables

Compression factor plotted using reduced
variables. Different curves are different TR
21
Virial Equation of State
Most fundamental and theoretically
sound Polynomial expansion Viral Expansion
0 at Boyle temperature
Used to summarize P, V, T data Also allow
derivation of exact correspondence between virial
coefficients and intermolecular interactions