Median of a triangle - PowerPoint PPT Presentation
Title:
Median of a triangle
Description:
The orthocenter is the point of concurrency of the 3 altitudes of a triangle ... Sketch the altitudes and find the orthocenter for each ... – PowerPoint PPT presentation
Number of Views:1786
Avg rating:3.0/5.0
Title: Median of a triangle
1
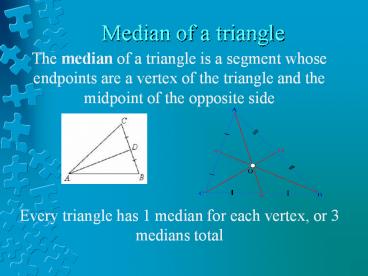
Median of a triangle
- The median of a triangle is a segment whose
endpoints are a vertex of the triangle and the
midpoint of the opposite side - Every triangle has 1 median for each vertex, or 3
medians total
2
Centroid of a triangle
- The centroid of a triangle is the point of
concurrency of the 3 medians of a triangle. - This point is also called the center of gravity
- When 3 or more lines intersect at 1 point, they
are called concurrent lines
3
Centroid theoremtheorem 32-1
- The centroid of a triangle is located 2/3 of the
distance from each vertex to the midpoint of the
opposite side - CP 2/3 CN
- BP 2/3 BM
- AP 2/3 AL
4
Using the centroid to find segment lengths
- LA 12, PN 3.1 Find AP
- AP 2/3 AL
- AP 2/3(12)
- AP 8
- Find NC
- CP 2/3CN
- CP PN CN
- 2/3 CN 3.1 CN
- 3.1 1/3 CN
- 9.3 CN
5
Finding the centroid on a coordinate plane
- Find the centroid of tri DEF with vertices
D(-3,5),E(-2,1), and F(-7,3) - Graph the triangle
- Find the midpoint of each segment -
- midp DF (-5,4), midp DE (-2.5,3)
- Since all 3 medians meet at the same point, the
intersection of any 2 will give the location of
the centroid.
6
- Find the equation of the line from point E to
- (-5,4) or from (-2,1) and (-5,4)
- Slope 3/-3 -1
- Y mxb so 1 -1(-2) b
- -1 b
y-x-1 - Find the equation of the line from point F to
- (-2.5,3) or from (-7,3) and (-2.5, 3)
- Slope is 0 so
- 3 -x-1
- 4 -x
- -4 x so centroid is (-4,3)
7
Find the centroid of tri RTSwith R(-2,2),
T(2,2), S(1, -2)
- Find the medians
- Find the equations of 2 lines
- Find the coordinate of the centroid
8
Altitude of a triangle
- The altitude of a triangle is the perpendicular
segment from the vertex to the line containing
the opposite side. - The orthocenter is the point of concurrency of
the 3 altitudes of a triangle
9
Locating the orthocenter
- Draw an acute, a right and an obtuse triangle
- Sketch the altitudes and find the orthocenter for
each - Is the orthocenter always in the interior of a
triangle?
10
Use graph paper
- Sketch the orthocenter of the triangle formed by
(4,2), (-1,1) and (1,6)
11
(No Transcript)