Geometric mean - PowerPoint PPT Presentation
Title:
Geometric mean
Description:
... altitude is drawn from the vertex of a right triangle's 90 degree angle to its ... AZ = YZ. YZ XZ. Find missing values a and b. a= 3 b=4. 3 5 4 5. 3. 5. 4 ... – PowerPoint PPT presentation
Number of Views:2385
Avg rating:3.0/5.0
Title: Geometric mean
1
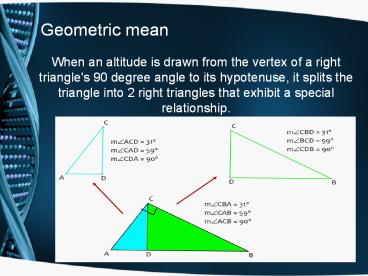
Geometric mean
- When an altitude is drawn from the vertex of a
right triangle's 90 degree angle to its
hypotenuse, it splits the triangle into 2 right
triangles that exhibit a special relationship.
2
Theorem 50-1
- If the altitude is drawn to the hypotenuse of a
right triangle, then the 2 triangles formed are
similar to the original triangle
3
CAUTION !!!
- Theorem 50-1 is only true if the altitude of the
right triangle has an endpoint on the hypotenuse,
not on the triangle's legs
4
Identifying similar right triangles
- Find RS and RQ,- Tri PQR is similar to Tri PSQ is
similar to Tri RSQ
P
S
3
5
4
R
Q
5
Finding geometric mean
- Sometimes , the means of a proportion are equal
to one another. - This is a special kind of proportion that can be
used to find the geometric mean of 2 numbers - The geometric mean for positive numbers a and b,
is the positive number x , such that
6
Another way to state geometric mean
- The geometric mean of a and b is equal to the
square root of the product of a and b, since - ab x2
7
Find the geometric mean
- Find the geometric mean of 3 and 12
- Find the geometric mean of 4 and 16
- Find the geometric mean of 2 and 9 in simplified
radical form. - Find the geometric mean of 5 and 11 to nearest
tenth.
8
Corollary 50-1-1
- If the altitude is drawn to the hypotenuse of a
right triangle, then the length of the altitude
is the geometric mean between the segments of the
hypotenuse
9
Corollary 50-1-2
- If the altitude is drawn to the hypotenuse of a
right triangle, then the length of a leg is the
geometric mean between the hypotenuse and the
segment of the hypotenuse that is closer to that
leg. - AZ YZ
- YZ XZ
10
Find missing values a and ba 3 b43 5
4 5
4
3
a
b
5
11
Find missing value for y
- 3 y
- y 4/3
y
4/3
3
12
(No Transcript)
13
(No Transcript)