Transformations

1
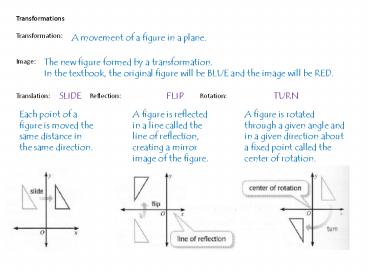
Transformations Transformation Image
Translation Reflection Rotation
A movement of a figure in a plane.
The new figure formed by a transformation. In
the textbook, the original figure will be BLUE
and the image will be RED.
SLIDE
FLIP
TURN
Each point of a figure is moved the same distance
in the same direction.
A figure is reflected in a line called the line
of reflection, creating a mirror image of the
figure.
A figure is rotated through a given angle and in
a given direction about a fixed point called the
center of rotation.
2
4. Draw a quadrilateral JKLM with vertices
J(-5, 3), K(-4, 5), L(-3, 3), and M(-4, 1).
Then find the coordinates of the vertices of the
image after the translation (x, y) ? (x 6 , y
2 ) and draw the image. Original Image J(-5,
3) ? K(-4, 5) ? L(-3, 3) ? M(-4, 1)
? Identify the transformation. If it is a
reflection, identify the line of reflection. If
it is a rotation, give the angle and direction
of rotation. 5. 6. 7.
3
center of rotation
The ____________________________for all rotations
in the textbook will be the origin. Rays drawn
from the center of rotation through corresponding
points on an original figure and its image form
an angle called the _____________________________.
Rotations are described by the angle and
direction of rotation, either _________________
or _________________________. NOTE a
complete circle (rotation) is Half of a
rotation is Begin with the light figure, and
rotate to the dark figure. Estimate the angle
and direction of rotation.
angle of rotation
clockwise
counterclockwise
4
Rotations in Coordinate Geometry Coordinate
notation for specific rotations. Rotat
ional Symmetry 5. Since you can rotate an
equilateral triangle three times within the
360 degree turn, divide 360 by 3 to find the
angle of rotation.