Binary Search Trees

1
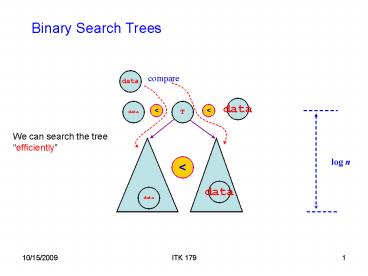
Binary Search Trees
data
compare
data
T
data
lt
lt
We can search the tree efficiently
log n
lt
data
data
2
What is the real benefit of using BST?
O(log2n)
Search 18, 2, 26
20
30
10
1
25
17
35
19
5
14
0
28
34
38
23
22
7
4
12
15
18
27
32
36
21
3
13
11
26
37
3
What is the benefit of using BST?
The average height of a binary search tree of n
nodes is
O(log2n)
if the n nodes are arrived based on a uniform
distribution on the space of possible keys.
This is as good as the binary search on a
sorted array. Proof not so difficult, not so
trivial..
f(n) The average internal path length of an
n-node BST
4
The average height of a BST
O(log2n)
f(n) The average internal path length of an
n-node BST
f(3) (323) / 3 2.67
0
0
1
1
1
1
2
2
0112
0123
0123
5
Analysis
Average Heights on n Random Keys
BST
How bad is the constant?
O(log2n)
? log2n O(log2log2n) ? 4.31101
Devroye and Reed,, SIAM J. Comput. 95
6
The sequence of node insertion will affect the
shape of the BST
1
Highly unbalanced BST
7
12
1, 7, 12, 25, 27, 13, 23, 17, 15
25
13
27
This situation is not uncommon e.g., the data is
roughly sorted.
23
17
15
7
Highly unbalanced BST
1
7
Balanced BST
12
17
25
13
27
13
25
7
15
23
27
23
17
1
12
15
8
AVL Trees (Ch 11.3, 11.4)
-- an example of Dynamic trees

• Adelson-Velskii and Landis, Soviet Mathematic
  Doklady, 31259-1263, 1962 C. Crane, D. Knuth,
  et al in 1970s

We dynamically maintain the properties of
AVL-tree when we insert (remove) a node by four
different operations (rotations)
Static trees
Dynamic trees
Huffman Code
-- an example of Static trees
We statically analyze the code and build up an
optimal tree for retrieving the code words.
9
AVL Tree
A BST in which the height difference between the
two children of any node is always less than 2.
1
1
-1
j
k
j1
k1
h
h1
10
Four operations (rotations)
performed at the bad node where the difference
between the heights of its two children is bigger
than 1 after insertion.
If a node is bad caused by
then perform

• RR rotation
• LL rotation
• RL rotation
• LR rotation

• Right-childs Right-child
• Left-childs Left-child
• Right-childs Left-child
• Left-Childs Right-child

11
No Rotation is Needed
1
0
-1
0
12
RR Rotations
2
1
13
RR Rotation
2
R
0
R
0
1
14
LL Rotation
L
-2
0
L
-1
0
15
Rotations RL
1
2
0
h1
0
-1
1
0
h1
0
-1
h
h
16
Rotations RL
RL Rotation
R
0
2
L
h1
-1
0
1
h1
-1
h1
h
h
h1
h
h
17
Rotations LR
LR Rotation
L
-2
0
1
h1
R
0
1
h1
-1
h1
h
h
-1
h1
h
h
18
Rotate this sub-tree first
2
R
Could be RR or RL, depending on what happens in
the blue sub-tree.
R
2
Afterwards, examine the red node again to see is
another rotation is needed.
19
Rotations LL
1
2
1
h1
-1
-2
-1
h
-1
-2
0
h-1
h
-1
0
h-1
h-1
20
Example
10
20
30
10
RR Rotation
20
20
10
30
30
21
Example
40
50
20
RR Rotation
20
10
30
40
10
40
50
30
50
22
Example
35
20
R
30
RL Rotation
40
10
40
L
20
50
30
50
10
35
35
23
Possible complications
Re-assign the links
2
h1
-1
h1
-1
h
h
Tracking the heights and balance-factors
24
RR rotation in JAVA
at
2
R
// RR rotation on t private void RR(TNodeltEgt
t) TNodeltEgt a t, b t.right
a.right b.left b.left a a.height -
2 return b
b
h
R
1
h
h
height is an extra member variable in the
TNodeltEgt.
25
RL rotation in C
at
// RL rotation on t private void RL(TNodeltEgt
t) TNodeltEgt a, b, c a t b
t.right c t.right.left a.right
c.left b.left c.right c.left a
c.right b c.height b.height--
a.height-2 return c
b
R
2
L
c
h1
-1
h1
-1
h
h
26
How to determine which rotation is needed?
RR
L L
R L
L R
2
-2
2
-2
-1
1
1
-1
27
AVL
h Average Heights n Random Keys