Public Key Encryption

1
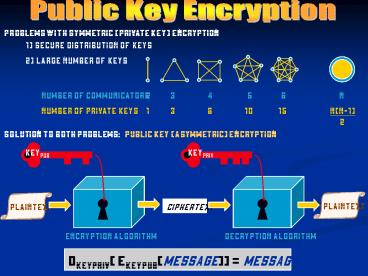
Public Key Encryption
Problems with symmetric (private key) encryption
1) secure distribution of keys
2) large number of keys
number of private keys
1
3
6
10
15
n(n-1) 2
Solution to both problems Public Key
(asymmetric) encryption
keypub
keypriv
DkeyPriv( EkeyPub(message)) message
2
Data transmission via public key encryption
Every user maintains a unique pair of keys one
private and one public.
Public keys are available for anyone to use.
For Sue to send a message to Bob, she first
encrypts using Bobs public key. This
ensures that only Bob will be able to read the
message.
Note that this preserves data confidentiality,
but does not ensure authenticity.
Public key encryption first proposed in 1976 -
Diffie Hellman
3
RSA Encryption
Rivest-Shamir-Adelman (1978) is the best known
of current public key encryption methods.
RSA poperties DkeyPriv(EkeyPub(message))
message DkeyPub(EkeyPriv(message))
message
Secure transmission 1) Sue encrypts the message
(or part of it) using her private key. 2) Sue
uses Bobs public key to encrypt the result of
(1). 3) The message is transmitted. 4) Bob
decrypts the message with his private key. 5)
Bob decrypts the result of (5) (or appropriate
part) with Sues public key.
The above mechanism preserves both
confidentiality and authenticity.
4
RSA Algorithm
Begin with two large primes (p and q).
n pq (Note that n should be about
200 digits - roughly 512 bits.)
Select e relatively prime to (p-1)(q-1).
Select d so that (ed) mod ((p-1)(q-1)) 1.
public key (e, n) private key (d, n)
Encryption Algorithm (apply to each part of the
transmission)
Ee(message) (messagee) mod n
Decryption Algorithm (apply to each part of the
transmission)
Dd(message) (messaged) mod n
Side note (p-1)(q-1) comes from Eulers
definition of totient ?(n) number of positive
integers less than n that are relatively prime to
n.
5
Example (note that numbers are artificially
small.)
p 2
q 17
Therefore, n pq 34
Select e 3
Note that (p-1)(q-1) 16. (3 and 16 are
relatively prime.)
d 11 because ed 311 33 and 33 mod 16
1
Treat alphabet as integers from zero, and include
blank
HI MOM SEND
3 2 32 28 24 28 32 18 30 21 27
3 2 32 28 24 28 32 18 30 21 27
7 8 26 12 14 12 26 18 4 13 3
6
More about RSA
Cryptanalysis Issues 1) The values of p, q, and
?(n) are not divulged. 2) Cryptanalysis of RSA
accomplished by finding the prime factors of a
200-digit number. 3) Factoring is not known to
be an NP problem, but the best known
algorithms are exponential. 4) To date no
serious security flaws have been discovered.
Finding p and q Verifying that p and q are
prime requires testing about 1050 potential
factors. A practical alternative (Solovay
Strassen algorithm) tests a number to
any desired probability of being prime.
Encryption Decryption RSA can be as much as
10,00 times slower than symmetric algorithms
(Multiplication used in place of bit manipulation
and table lookup/indexing). to improve
computation (a b) mod n (a mod n) (b
mod n) mod n