Sparse MatrixVector Multiplication

1
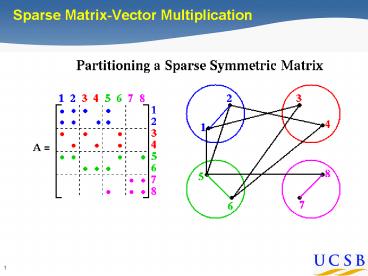
Sparse Matrix-Vector Multiplication
2
Clustering benchmark graph
3
Link analysis of the web

• Web page vertex
• Link directed edge
• Link matrix Aij 1 if page i links to page j

4
Web graph PageRank (Google)
Brin, Page
An important page is one that many important
pages point to.

• Markov process follow a random link most of the
  time otherwise, go to any page at random.
• Importance stationary distribution of Markov
  process.
• Transition matrix is pA (1-p)ones(size(A)),
  scaled so each column sums to 1.
• Importance of page i is the i-th entry in the
  principal eigenvector of the transition matrix.
• But, the matrix is 8,000,000,000 by 8,000,000,000.

5
A Page Rank Matrix

• Importance ranking of web pages
• Stationary distribution of a Markov chain
• Power method matvec and vector arithmetic
• MatlabP page ranking demo (from SC03) on
  a web crawl of mit.edu (170,000 pages)

6
Strongly connected components

• Symmetric permutation to block triangular form
• Find P in linear time by depth-first search
  Tarjan

7
RMAT Approximate Power-Law Graph
8
Strongly Connected Components
9
Sparse Adjacency Matrix and Graph
?
AT
x
ATx

• Adjacency matrix sparse array w/ nonzeros for
  graph edges
• Storage-efficient implementation from sparse data
  structures

10
Breadth-First Search Sparse mat vec
?
AT
x
ATx

• Multiply by adjacency matrix ? step to neighbor
  vertices
• Work-efficient implementation from sparse data
  structures

11
Breadth-First Search Sparse mat vec
?
AT
x
ATx

• Multiply by adjacency matrix ? step to neighbor
  vertices
• Work-efficient implementation from sparse data
  structures

12
Breadth-First Search Sparse mat vec
?
AT
x
ATx

• Multiply by adjacency matrix ? step to neighbor
  vertices
• Work-efficient implementation from sparse data
  structures

13
Sparse Matrix times Sparse Matrix

• Shows up often as a primitive.
• Graphs are mostly not mesh-like, i.e. geometric
  locality and good separators.
• On a 2D processor grid, the parallel sparse
  algorithm looks much like the parallel dense
  algorithm.
• Redistribute to round-robin cyclic or random
  distribution for load balance.

14
Load Balance Without Redistribution
15
Load Balance With Redistribution