Draw a histogram to represent these data

1
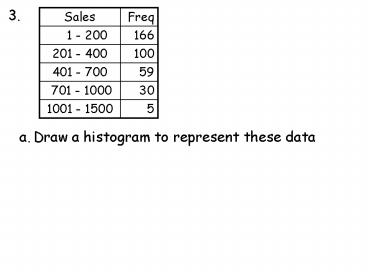
3.

• Draw a histogram to represent these data

2
3.

• Draw a histogram to represent these data

3
3.
b. Use interpolation to estimate the median and
interquartile range
4
3.
360 2 180 ? The median (Q2) is at the 180th
piece of data. In the 201 400 class
b. Use interpolation to estimate the median and
interquartile range

Q2 14 x 200 100 200.5 Q2 228.5
Class Frequency
Class Width
5
3.
360 4 90 ? The lower quartile (Q1) is at the
90th piece of data. In the 1 200 class
b. Use interpolation to estimate the median and
interquartile range

Q1 90 x 200 166 0.5 Q1 108.9
Class Frequency
Class Width
6
3.
c. Estimate the mean and standard deviation
7
3.
c. Estimate the mean and standard deviation The
estimated mean 110980 360
? ? 308.8
8
3.
Standard Deviation Calculate the mean of the
squares minus the square of the mean then find
the square root of this value
c. Estimate the mean and standard
deviation Standard deviation v(58105890 360
3082) ? s 258
Mean 308
9

• A keep fit enthusiast swims, runs or cycles each
  day with a probabilities 0.2, 0.3 and 0.5
  respectively. If he swims then he spends time in
  the sauna with a probability of 0.35. The
  probability that he spend time in the sauna after
  running or cycling is 0.2 and 0.45 respectively.
• Represent this on a tree diagram
• Find the probability that on any particular day
  he uses the sauna
• Given that he uses the sauna, find the
  probability that he has been swimming on that day
• Given that he did not use the sauna one day, find
  the probability that he has been swimming

10

• A keep fit enthusiast swims, runs or cycles each
  day with a probabilities 0.2, 0.3 and 0.5
  respectively. If he swims then he spends time in
  the sauna with a probability of 0.35. The
  probability that he spend time in the sauna after
  running or cycling is 0.2 and 0.45 respectively.
• Represent this on a tree diagram

0.07
0.35
S
W
0.65
0.13
0.2
NS
0.2
S
0.06
0.3
R
0.8
0.24
NS
0.5
0.45
S
0.225
C
0.55
0.275
NS
11
b) Find the probability that on any particular
day he uses the sauna
P(sauna) 0.07 0.06 0.225 ? P(sauna)
0.355
0.07
0.35
S
W
0.65
0.13
0.2
NS
0.2
S
0.06
0.3
R
0.8
0.24
NS
0.5
0.45
S
0.225
C
0.55
0.275
NS
12
c) Given that he uses the sauna, find the
probability that he has been swimming on that day
P(W ? S) P(WS) x P(S) 0.07 P(WS) x
0.355 P(WS) 0.197 ? 0.20
P(S) 0.355
0.07
0.35
S
W
0.65
0.13
0.2
NS
0.2
S
0.06
0.3
R
0.8
0.24
NS
0.5
0.45
S
0.225
C
0.55
0.275
NS
13
d) Given that he did not use the sauna one day,
find the probability that he has been swimming
P(W ? NS) P(WS) x P(NS) 0.13 P(WNS) x
0.645 P(WNS) 0.202
P(NS) 0.645
0.07
0.35
S
W
0.65
0.13
0.2
NS
0.2
S
0.06
0.3
R
0.8
0.24
NS
0.5
0.45
S
0.225
C
0.55
0.275
NS
14
The events A and B are such that P(A) 0.4
P(B) 0.5 and P(AB) 0.8
Multiplication Rule
i) Find P(A ? B) P(A ? B) P(AB) x P(B) P(A
? B) 0.8 x 0.5 P((A ? B) 0.4
P(B) 0.5 P(B) 0.5
15
The events A and B are such that P(A) 0.4
P(B) 0.5 and P(AB) 0.8
P(A ? B) 0.4
ii) Find P(A ? B) Since P(A) 0.4 From the
Venn diagram P(A ? B) 0
A
B
0.4
16
The events A and B are such that P(A) 0.4
P(B) 0.5 and P(AB) 0.8
Addition Rule
iii) Find P(A U B) P(A U B) P(A) P(B) P(A ?
B) P(A U B) 0.4 0.5 - 0 P((A U B) 0.9
P(A ? B) 0
17
The events A and B are such that P(A) 0.4
P(B) 0.5 and P(AB) 0.8
Multiplication Rule
iv) Find P(AB) P(A ? B) P(AB) x P(B) 0
P(AB) x 0.5 P(AB) 0
P(A ? B) 0
18

• b) State with a reason whether or not the events
  A and B are mutually
• exclusive
• independent
• i) The results are mutually exclusive because P(A
  ? B) 0
• ii) If P(B) ? P(AB) or P(A) ? P x P(BA) or P(A
  x P(B) ? P(A ? B) then P(A) and P(B) are not
  independent i.e the events A and B are not
  independent