Hash Tables

1
Hash Tables
2
Overview

• What are hash tables ?
• what
• why
• operations
• - key words collision, hash function
• Implementation 1 open addressing
• Implementation 2 chained lists

3
Definition

• A hash table is a data structure that uses a hash
  function to efficiently map certain identifiers
  or keys to associated values
• In a hash table
• A container/collection i.e. an object that holds
  a bunch of other objects (just like arrays,
  lists, stacks, queues, trees and graphs)
• VALUES are associated with KEYS
• (just as values in an array are associated with
  an index, values in a list are associated with a
  position)
• Hashing function
• A hash function maps a search key into an integer
  between 0 and n-1.
• A single integer that may serve as an index into
  an array.
• The values returned by a hash function are called
  hash values, hash codes, hash sums, or simply
  hashes.

4
Why?

• Using balanced trees AVL trees) we can implement
  table operations (retrieval, insertion and
  deletion) efficiently. ? O(logN)
• Can we find a data structure so that we can
  perform these table operations better than
  balanced search trees? ? O(1)
• In a hash table
• Searching for a value is O(1) ie constant time
• Inserting a value is O(1)
• Better than a binary search tree!

5
How?

• Uses an array to store data
• The position of an item in the array is computed
• Using a hash function applied to the key i.e.
• position hashFunction(key)
• Example hash functions
• ASCII value of first letter 65 MOD array size
• sum of digits in student number MOD array size
• Store values in the array (open addressing) or
• store lists in the array (chained lists)

6
Problems

• Will two keys map to the same location in the
  table?
• How to decide the size of the table?
• If the data set is of known size
• a perfect hashing function can be used, then the
  table can be made as the size as the data set.
• Otherwise, , to make the table 150 the size of
  the dataset.
• If we do not know the size of the data set
• Dynamic resizing
• When to resize?
• Can we simply expand the table when it is full?

7
Terminology

• Perfect hashing function
• A hashing function that maps each element to a
  unique position in a table.
• Collision
• The situation where two elements or keys map to
  the same location in the table
• Dynamic resizing
• Dynamics resizing of a hash table involves
  creating a new hash table that is larger than the
  original, inserting all of the elements of the
  original table into the new table, and then
  discarding the original one.
• Load factor
• The ratio of the number of elements in a hash
  table to its size
• Used to describe how full the table currently is

8
Hashing Functions

• We do not need the hashing function to be perfect
  to get good performance from the hash table
• Have a function that does reasonably good job of
  distributing our elements in the table such that
  we avoid collisions.
• A reasonably good hashing function will still
  result in constant time access
• Examples
• ASCII value of the first letter MOD array size
• Sum of digits MOD array size
• Division use the remainder of the key divided by
  some positive integer (table size for example) as
  the index of the given element

Hashcode(key) Math.abs(key)size
9
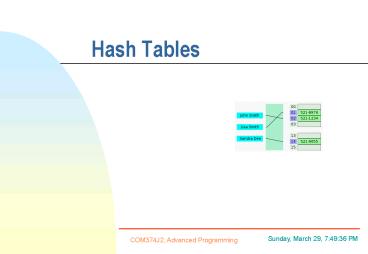
Resolving collisions Chaining

• Definition
• The chaining method for handling collisions
  simply treats the hash table conceptually as a
  table of collection rather than as a table of
  individual cells.
• Uses an array of lists
• Key and hash function used to compute location
  which list the value will be stored in
• Each cell in the hash table would be something
  like the LinearNode class
• Advantages
• No problems with collisions as values are just
  added to the end of the appropriate list
• Hash table never be full
• Disadvantages
• Need to use lists, Constructing new chain nodes
  is relatively expensive
• Parts of the array might never be used.
• As chains get longer, search time increases to
  O(n) in the worst case.

10
Example
11
Resolving Collision Open Addressing

• Definition
• The open addressing method for handling
  collisions looks for another open position in the
  table rather than the one to which the element is
  originally hashed.
• Values stored directly in the array - ie an array
  of Objects
• Problem
• collisions two keys compute to the same location
• Solutions
• linear probing look in slots pos1, pos 2,
  pos3,pos4 etc. (i.e. use next available free
  slot)
• Quadratic probing look in slots pos1, pos4,
  pos9, pos16 etc
• Rehash
• calculate another position

12
Examples
13
Linear probing

• In linear probing, we search the hash table
  sequentially starting from the original hash
  location.
• If a location is occupied, we check the next
  location
• We wrap around from the last table location to
  the first table location if necessary.
• Advantages
• Simple to implement
• Disadvantages
• Tends to create clusters of filled position
  within the table
• These clusters will affect the performance of
  insertions/search
• Deletion becomes trickier.
• The array can become full

14
Linear probing an Example

• If the hash table is not full, attempt to store
  key in the next array element (t1)N, (t2)N,
  (t3)N until you find an empty slot
• Example
• Table Size is 11 (0..10)
• Hash Function h(x) x mod 11
• Insert keys 20, 30, 2, 13, 25, 24, 10, 9

10
0
15
Quadratic Probing

• In quadratic probing,
• We start from the original hash location i
• If a location is occupied, we check the locations
  i12 , i22 , i32 , i42 ...
• We wrap around from the last table location to
  the first table location if necessary
• Advantages and disadvantages
• Tends to distribute keys better than linear
  probing
• Alleviates problem of clustering
• Time consuming calculating new probe position
• Runs the risk of an infinite loop on insertion
  and might not find free space for item even if
  table not full
• Consider inserting the key 16 into a table of
  size 16, with positions 0, 1, 4 and 9 already
  occupied - table size should be prime.
• Deletion becomes trickier.

16
Quadratic Probing an Example

• If the hash table is not full, attempt to store
  key in the next array element (t12)N,
  (t22)N, (t32)N until you find an empty slot
• Example
• Table Size is 11 (0..10)
• Hash Function h(x) x mod 11
• Insert keys 20, 30, 2, 13, 25, 24, 10, 9

10
0
17
Double Hashing

• Resolving collisions by providing a secondary
  hashing function, h2, to be used when the primary
  hashing function, h1, results in a collision.
• Basic requirement
• h2(key) ? 0
• h1 ? h2
• Implementation Let a second hash function
  h2(key)d. Attempt to store key in array
  elements (td)N, (t2d)N, (t3d)N until you
  find an open slot.
• Using the division method to maintain the
  calculated index within the bounds of the table

18
Double Hashing an Example

• Typical second hash function
• h2(x)R - ( x R )
• where R is a prime number, R lt N (size of the
  table)
• Example
• Table Size is 11 (0..10)
• Hash Function
• h1(x) x mod 11
• h2(x) 7 (x mod 7 )
• Insert keys 20, 30, 2, 13, 25, 24, 10, 9

19
Open Addressing Retrieval Deletion

• In open addressing, to find an item with a given
  key
• We probe the locations (same as insertion) until
  we find the desired item or we reach to an empty
  location.
• Deletions in open addressing cause complications
• Examples elements Ann, Andrew, and Amy all
  mapped to the same location in the table and
  collision was resolved using linear probing. What
  happens if we now remove Andrew?

Ann
Bob
Andrew
Doug
Bill
Amy
20
Solutions

• Solution To mark items as deleted but not
  actually remove them from the table until some
  future point when the deleted element is
  overwritten by
• A new inserted table
• The entire table is rehashed.
• Each cell is in one of 3 possible states
• active
• empty
• deleted
• For Find or Delete
• only stop search when EMPTY state detected (not
  DELETED)

• A deleted location will be treated as an occupied
  location during retrieval and insertion.

21
Hash Table Operations

• public
• insert(key, item)
• store the item in the hash table at the position
  dictated by the key
• delete(key)
• delete the item in the hash table at the position
  dictated by the key
• fetch(key) -gtitem
• get the item in the hash table at the position
  dictated by the key
• private
• hashFunction(key) gtposition
• calculate the position for the given key

22
Java Implementation
interface HashTable public void put(String
key, Object value) public Object get(String
key) public void remove(String key)
23
DataItem
class DataItem private String key private
Object value private boolean
deleted DataItem(String key, Object
value) this.key key this.value
value deleted false public String
getKey() return key public Object
getValue() return value public void
markDeleted()deleted true public boolean
isDeleted()return deleted
24
HashTable Java Implementation

• OpenAddrHashTable
• implements HashTable
• private DataItem values
• Constructor
• Implementation three methods

• ChainHashTable
• implements HashTable
• private LinkedListltDataItemgt values
• Constructor
• Implementation three methods