Binary Trees - PowerPoint PPT Presentation
1 / 25
Title:
Binary Trees
Description:
In an array, linear search (an O(N) algorithm) or binary search (an O(log N) ... data to the left is smaller and the data to the right is larger (alphabetically) ... – PowerPoint PPT presentation
Number of Views:45
Avg rating:3.0/5.0
Title: Binary Trees
1
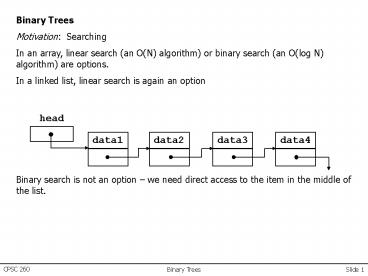
Binary Trees Motivation Searching In an array,
linear search (an O(N) algorithm) or binary
search (an O(log N) algorithm) are options. In a
linked list, linear search is again an option
Binary search is not an option we need direct
access to the item in the middle of the list.
2
A binary search tree gives us access to the
middle element of a collection
- At each node in the tree, the data to the left is
smaller and the data to the right is larger
(alphabetically). - Searching for J
- Start at the root of the tree (G)
- J is greater than G so discard the left half of
the tree - just like binary search! - Consider K, J is smaller than K, so discard the
right half of the remaining tree.
3
Definition A binary tree is a structure that is
either empty or consists of a node called a root
and two binary trees called the left sub-tree and
right sub-tree. Note that this definition is
recursive we define a binary tree as a
structure that consists of two other (sub) trees.
4
Domain a set of nodes containing one data item
and two pointers to other nodes (the set could be
empty). Structure there is a unique root node
(that has no parent node) having zero, one or two
child nodes every other node has exactly one
parent node and either zero, one or two child
nodes Operations insertLeft, insertRight -
insert to left or right of given nodefind find
node containing given itemfindParent find
parent of given nodedeleteItem remove node
containing given itemprint print data in
tree not an exhaustive list
5
Some terminology The path from node N1 to node
Nk is a sequence of nodesN1, N2, , Nk where Ni
is the parent of Ni1. The length of the path is
the number of edges in the path (some texts use
the number of nodes rather than number of
edges). The depth or level of a node N is the
length of the path from the root to N. The level
of the root is 0. A leaf is a node that has no
children. The height of a node N is the length of
the longest path from N to a leaf node. The
height of a leaf node is 0. The height of a tree
is the height of the root node. The number of
nodes in a tree of height h is at least h1 but
no more than 2h1-1. This can be proved by
induction.
6
Height of tree Depth of node containing
2 Height of node containing 2
7
Implementation of a binary tree in C Assume
that Item_type is the type of data stored in the
tree. Each node contains an item, a pointer to
the left sub-tree and a pointer to the right
sub-tree struct BNode Item_type item
BNode left BNode right A complete
implementation of a binary tree toolkit is
available in the examples section of the web.
8
As with the linked list toolkit, a makeNode
function will create a new BNode as
needed BNode makeNode( const Item_type item,
BNode leftChild NULL, BNode rightChild
NULL )// Pre item is valid, leftChild points
to a node or// is NULL and rightChild points to
a node or is NULL// Post a new node is created
and its address is// returned
9
As with the linked list toolkit, a makeNode
function will create a new BNode as
needed BNode makeNode( const Item_type item,
BNode leftChild NULL, BNode rightChild
NULL )// Pre item is valid, leftChild points
to a node or// is NULL and rightChild points to
a node or is NULL// Post a new node is created
and its address is// returned BNode
result result new BNode result-gtitem item
result-gtleft leftChild result-gtright
rightChild return result
10
insertLeft Insert an item to the left of a node
(or create a new tree). We assume that current
does not already have a left child so we are
inserting into an empty slot in the tree. void
insertLeft( BNode current, const
Item_type item )// PRE current points to a
node in a binary tree or// is NULL// POST if
current is not null the left child of// current
is a new node containing item otherwise//
current points to a root node containing item
11
insertLeft Insert an item to the left of a node
(or create a new tree). We assume that current
does not already have a left child so we are
inserting into an empty slot in the tree. void
insertLeft( BNode current, const
Item_type item )// PRE current points to a
node in a binary tree or// is NULL// POST if
current is not null the left child of// current
is a new node containing item otherwise//
current points to a root node containing item
if ( current NULL ) current
makeNode( item, NULL, NULL ) else
current-gtleft makeNode( item, NULL, NULL )
12
deleteItem The task of removing a node from a
binary tree is quite complicated. We will break
the task down into smaller sub-tasks in a
top-down fashion. bool deleteItem( BNode root,
const Item_type item )// Pre root points to
the root of a binary tree or is// NULL// Post
if item is in tree, first instance of node//
containing item has been deleted and true
returned// otherwise false returned
13
deleteItem The task of removing a node from a
binary tree is quite complicated. We will break
the task down into smaller sub-tasks in a
top-down fashion. bool deleteItem( BNode root,
const Item_type item )// Pre root points to
the root of a binary tree or is// NULL// Post
if item is in tree, first instance of node//
containing item has been deleted and true
returned// otherwise false returned
BNode target find( root, item ) if(
target NULL ) return false else
deleteNode( target ) return true
14
find a helper function for deleting an item from
the tree. In order to delete an item, we need to
find the node that contains it. Be aware that we
need a reference to the pointer that points to
this node if we are going to be able to link the
tree up correctly when the node is deleted.
BNode find( BNode root, const Item_type
item ) // PRE root points to the root of a
binary tree// POST if item is in the tree, the
address of the// node containing item is
returned otherwise, // NULL is returned
15
find a helper function for deleting an item from
the tree. In order to delete an item, we need to
find the node that contains it. Be aware that we
need a reference to the pointer that points to
this node if we are going to be able to link the
tree up correctly when the node is deleted.
BNode find( BNode root, const Item_type
item ) // PRE root points to the root of a
binary tree// POST if item is in the tree, the
address of the// node containing item is
returned otherwise, // NULL is returned if
( root NULL root-gtitem item )
return root BNode result find(
root-gtleft, item ) if ( result ! NULL )
return result else return find(
root-gtright, item )
16
Now we have a reference to the pointer to the
node to be deleted, we will write deleteNode.
Before we implement this function we will develop
an algorithm Case 1 node to be deleted does
not have a left child
Case 2 node to be deleted does not have a right
child
17
Case 3 node to be deleted has both a left and
right child. This is the tricky one. There is
no obvious way to remove a node having two
children and re-connect the tree. Instead, we
will choose not to delete the node but rather
copy data from a lower node into the current
node. We will arbitrarily choose to copy data
from the left child of the current node.
18
void deleteNode( BNode target )// Pre target
points to a node in the tree// Post node
pointed to by target has been removed// from
tree BNode tempPtr target if(
target-gtleft NULL ) target
target-gtright delete tempPtr else
if( target-gtright NULL ) target
target-gtleft delete tempPtr else
target-gtitem target-gtleft-gtitem
deleteNode( left )
19
Tree Traversal There are three common types of
binary tree traversal Preorder visit the
current node, then its left sub-tree, then its
right sub-tree Inorder visit the left
sub-tree, then the current node, then the right
sub-tree Postorder visit the left sub-tree,
then the right sub-tree, then the current node
20
Preorder visit the current node, then its left
sub-tree, then its right sub-tree
Data printed using preorder traversal 5 8
2 9 4 3 0 1 6 7
21
Inorder visit the left sub-tree, then the
current node, then the right sub-tree
Data printed using inorder traversal 2 9 8
4 5 0 1 6 3 7
22
Postorder visit the left sub-tree, then the
right sub-tree, then the current node
Data printed using postorder traversal 9 2
4 8 6 1 0 7 3 5
23
Inorder traversal void inorder( BNode root,
void ( visit )( BNode ) )// Pre root points
to a binary tree or is NULL// Post function
visit has been applied to each node// in the
tree using inorder traversal if (root !
NULL) inorder preorder
postorder inorder(root-gtleft, visit) (1)
(2) (1) visit(root) (2)
(1) (3) inorder(root-gtright, visit) (3)
(3) (2) The implementation of
functions to perform preorder and postorder
traversal is left as an exercise.
24
Application Binary Expression Trees Arithmetic
expressions can be represented using binary
trees. We will build a binary tree representing
the expression ( 3 2 ) 5 1 We start by
identifying the operator with the highest
precedence and build a binary tree having the
operator at the root, the left operand as the
left sub-tree and the right operand as the right
sub-tree. We continue in this fashion until all
operators have been represented (3 2 ) (3
2) 5
25
(3 2) 5 1 Now lets print this
expression tree using postorder traversal
3 2 5 1 - What we now have is the arithmetic
expression written usingreverse Polish notation
(after Jan Lukasiewicz) It is much easier to
write an algorithm to evaluate an expression
written in this form. We saw this in one of the
labs