Chapter 4 PPT

1
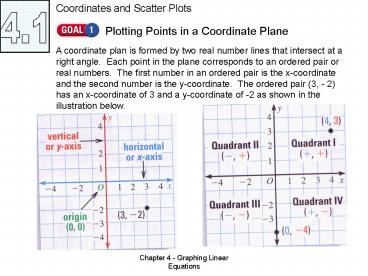
Coordinates and Scatter Plots
4.1
A coordinate plan is formed by two real number
lines that intersect at a right angle. Each
point in the plane corresponds to an ordered pair
or real numbers. The first number in an ordered
pair is the x-coordinate and the second number is
the y-coordinate. The ordered pair (3, - 2) has
an x-coordinate of 3 and a y-coordinate of -2 as
shown in the illustration below.
2
(No Transcript)
3
USING MULTIPLICATION IN REAL LIFE
Many real-life situations can be described in
terms of pairs of numbers. Medical charts record
both the height and weight of the patients, while
weather reports may include both temperature and
windspeed. One way to analyze the relationships
between two quantities is to graph the pairs of
data on a coordinate axis. Such a graph is
called a scatter plot.
4
Graphing Linear Equations
4.2
A solution of an equation in two variables x and
y is an ordered pair (x, y) that makes the
equation true. The graph of an equation in x and
y is the set of all points (x, y) that are
solutions of the equation. The graph of a
linear equation is a straight line.
When you make a table of values to graph an
equation, you may want to choose values for x
that include negative values, zero, and positive
values. This way you will see how the graph
behaves to the left and right of the y-axis.
The solution of an equation such as 2x 1 3 is
a real number. Its graph is a point on the real
number line. The equation y 2 3x is a linear
equation in two variables. Its graph is a
straight line.
5
(No Transcript)
6
Horizontal and Vertical Lines
All linear equations in x and y can be written in
the form Ax By C. When A 0 the equation
reduces to By C and the graph is a horizontal
line. When B 0 the equation reduces to Ax C
and the graph is a vertical line.
7
Use the graph to decide whether the point lines
on the graph of 4 x y 8. Justify your
answer algebraically.

• (1, 4)
• (3, 4)

8
Use a table of values to graph the equation 5 x
y - 2
9
Graph the equation y 2
10
Graph the equation x -3
11
Graphing Linear Equations
4.3
You can graph an equation by using a different
method. In the last section, we used a table to
substitute in numbers. Now we are going to graph
by finding out where the line crosses the x and y
axis.
The point in which the line crosses the y axis is
the y intercept and the point in which the line
crosses the x axis is the x intercept
12
Example
Finding Intercepts
Find the x-intercept and the y-intercept of the
graph of the equation
The intercepts occur at zero, so substitute in
zero
Solution
The x-intercept is 3. The line crosses at point
(3,0)
The y-intercept is 2. The line crosses at point
(0,2)
13
Notice how the line cross at these points. The
graph represents the equation of 2 x 3 y 6
14
Remember
Draw your graphs to scale.
Graph the equation
Example
15
Use a graph to solve a real life problem. You
are organizing the annual spaghetti dinner to
raise funds for a zoo. Your goal is to sell
1500 worth of tickets. Assuming 200 adults and
100 students will attend the dinner, how much
should you charge for and adult and student
ticket.
Example
16
Graphing Linear Equations
4.4
The slope (m) of a line is the number of units
theline rises or falls for each unit of
horizontal change from left to right. Slope
Rise/run often called rise over run.
You can find slope by using the following
equation.
17
Mgt0
A line with a positive slope with rise A line
with a negative slope falls. A line with a zero
slope is horizontal. A line that doesnt have a
slope is vertical. (Undefined)
Mlt0
M0
M(Undefined)
18
Graphing Linear Equations
4.5
Two variables x and y vary directly if there is a
nonzero number k such that the following is true.
This is true for a line that travels through the
origin (0, 0) y k x
k in this scenario is the same is m
(or slope) The number k is the constant of
variation. Two quantities that vary directly are
said to have direct variation.
The variation of the equation or model is the
slope of the line.
19
Find the constant of variation for the following
graph. Step 1 Find the Slope Step 2 The
slope is the constant of variation.
Example
(3, 2)
(-3, -2)
20
Graphing Linear Equations
4.6
The linear equation
is written in slope-intercept form. The
slope of the line is m. The y-intercept is b.
It is called this because you can read the slope
and y-intercept from the equation.

The y intercept is 3 and the slope is 2 . Do
you see why? By transforming the equation into
slope intercept form you can always pick out
the slope and y intercept.
Parallel lines are lines that do not intersect.
Any two vertical lines are parallel. Any two
non-vertical lines are parallel if and only if
they have the same slope.
21
4.7
Remember that in the form y m x b (b) is the
y-intercept and m is the slope. The X intercept
is the solution to the equation.
22
4.8
Remember In order for it to be a function, you
can have exactly one output for any given input.
If there are multiple outputs for the given
input, you have what is called a relation.
23
Using Function Notation
We can use f(x) Functional Notation to
represent y. In general the f(x) READ F of
x replaces the y to represent a function. In the
case of a function the f(x) replaces the y, so
that the ordered pairs are (x, f(x)) In a
function the x is the input (domain) and y is the
output (range). Remember from earlier You
graph a linear function the same way you graph a
linear equation. Replace the f(x) for y and use
the principals learned previously to pick out the
y-intercept and the slope.
Graph f(x) 1/2x 3