2D coordinates

1
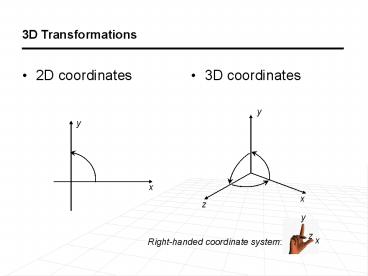
3D Transformations

• 2D coordinates

• 3D coordinates

y
y
x
x
z
Right-handed coordinate system
2
3D Transformations (cont.)
1. Translation in 3D is a simple extension from
that in 2D 2. Scaling is similarly
extended
3
3D Transformations (cont.)
3. The 2D rotation introduced previously is just
a 3D rotation about the z axis. similarly
we have
4
Composition of 3D Rotations
In 3D transformations, the order of a sequence
of rotations matters!
5
More Rotations
We have shown how to rotate about one of the
principle axes, i.e. the axes constituting the
coordinate system. There are more we can do, for
example, to perform a rotation about an arbitrary
axis
We want to rotate an object about an axis in
space passing through (x1, y1, z1) and (x2, y2,
z2).
Y
X
Z
6
Rotating About An Arbitrary Axis
Y
Y
P2
P1
?
P1
Z
X
Z
P2
X
1). Translate the object by (-x1, -y1, -z1)
T(-x1, -y1, -z1)
2). Rotate the axis about x so that it lies on
the xz plane Rx(?)
Y
Y
P1
P1
?
X
Z
P2
X
Z
P2
3). Rotate the axis about y so that it lies on
z Ry (?)
4). Rotate object about z by ? Rz(?)
7
Rotating About An Arbitrary Axis (cont.)
After all the efforts, dont forget to undo the
rotations and the translation! Therefore, the
mixed matrix that will perform the required task
of rotating an object about an arbitrary axis is
given by M T(x1,y1,z1) Rx(-?)Ry(-?) Rz(?)
Ry(?) Rx(?)T(-x1,-y1,-z1)
Finding ? is trivial, but what about ?? The
angle between the z axis and the projection of P1
P2 on yz plane is ?.
Y
P2
?
P1
X
Z