Example of Constructing the DAG

1
Example of Constructing the DAG

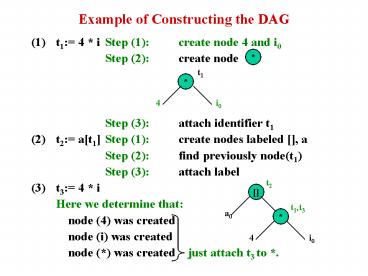
• t1 4 i Step (1) create node 4 and i0
• Step (2) create node
• Step (3) attach identifier t1
• t2 at1 Step (1) create nodes labeled , a
• Step (2) find previously node(t1)
• Step (3) attach label
• t3 4 i
• Here we determine that
• node (4) was created
• node (i) was created
• node () was created just attach t3 to .

t1

i0
4
t2

t1,t3
a0

i0
4
2
Common Subexpression Elimination

• Example
• a b c
• b a d
• c b c
• d a - d

c

a b c b a d c b c d b
b,d
-
d0
a

c0
b0

• Detection Common subexpressions can be detected
  by noticing, as a new node m is about to be
  added, whether there is an existing node n with
  the same children, in the same order, and with
  the same operator.
• if so, n computes the same value as m and may be
  used in its place.
• Note The expressions bc in (1) and (3) are not
  confused.

3
Dead Code Elimination

• Transfomation if x is dead (i.e., not live)
  never subsequently
• used after a point where statement x y z
  appears in a basic block. Then, this statement
  may be safely removed.

e
Examples
c


a bc bb-d ccd ebc
ab c da - d cd c
a
b
c
b,d
-

-

d0
a

c0
d0
b0
c0
b0
b is not used at the exit of the basic block

• Method Delete from the DAG any root (node with
  no ancestors) that has no live variable. Weaker
  form delete (when multiple) dead variable label.
  Repeat until we remove all nodes (labels) that
  correspond to dead code.

4
Renaming Temporary Variables
Example (1) t b c (1) u b c
rename
t
u
Change (rename) label


b0
c0
b0
c0

• Normal Form Each statement that defines a
  temporary, defines a new temporary.
• - A basic block can always be transformed into
  an equivalent block which is in normal form

5
Interchange of Statements

• Example
• t1 b c
• t2 x y

t1
t2


b0
c0
x0
y0

• Observation We can interchange the statements
  without affecting the value of the block if and
  only if neither x nor y is t1 and neither b nor c
  is t2, i.e. we have two trees.
• Note Normal-form basic blocks permit all
  statement interchanges that are possible.

6
Algebraic Transformations

• Reduction in strength
• x 2 x x
• 2.0 x x x
• x / 2 x 0.5
• - Replace an expensive operator with a cheaper
  one.
• Constant folding
• 2 3.14 6.28
• -Evaluate constant expression at compile time

• Arithmetic Identities
• x 0 0 x x
• x 0 x
• x 1 1 x x
• x / 1 x
• - Replace left-hand side with simples right
  hand side.
• Associative/Commutative laws
• x (y z) (x y) z
• x y y x

Methodology Before we create a node of the DAG
we check whether such a node exists modulo the
above identities.
7
Global Data Flow Analysis

• To do code generation and optimization a compiler
  needs to collect information about the program as
  a whole and to distribute this information to
  each block in the flow-graph.
• Data flow analysis the process by which the
  compiler collects data-flow information.
• - by setting up and solving systems of equations
  that relate information at various points in the
  program.
• Example (generic) outS genS U (inS
  killS)

Information killed by the exec. of S
Information flowing after the execution of S
Generated by execution of S
Information flowing at the beginning of S
Note Sometimes information flows backwards inS
outS
8
Points and Paths

• Points
• between two adjacent statements within a block
• before the first statement
• after the last statement

d1
B
i m-1
d1 i m-1 d2 j n
d2
j n
flow-graph
State machine

• Paths Consider all points in all the blocks. A
  path from p1 to pn is a sequence of points p1, ,
  pn such that for each i?1, n-1
• - pi is the point immediately preceding a
  statement and pi1 is the point immediately
  following that statement in the same block, or
• - pi is the end of some block and pi1 is the
  beginning of a successor block.

9
Example of DFA Problem Reaching Definitions

• Definition of variable x is a statement that
  assigns or may assign a value to x.
• - unambiguous definitions assignment to x or
  read store a value in x from an I/O device.
• - ambiguous definitions may define the value of
  x
• procedure call with x as a parameter or global
  variable.
• assignment through a pointer.
• Definition d reaches a point p if there is a path
  from the point immediately following d to p such
  that d is not killed along that path.
• Killing a definition of a variable x happens if
  between two points along the path there is a
  definition of x.

10
Reaching Definition (Cont)

• Inaccuracies When defining reaching definition
  we sometimes allow inaccuracies.
• Undecidability to decide in general whether each
  path in a flow graph can be taken is an
  undecidable problem.
• Conservative inaccuracy an inaccuracy is
  conservative if it never leads to a change in
  what the program computes.
• - it is normally conservative to assume that a
  definition can reach a point even if it may not.
• - we allow definitions to pass through ambiguous
  definitions.

11
DF Analysis of Strongly Structured Programs

• gens d
• kills Da d
• outs gens ? (ins \ kills)
• gens gens2 ? (gens1 kills2)
• kills kills2 ? (kills1 gens2)
• ins1 ins, ins2 outs1
• outs outs2
• gens gens1 ? gens2
• kills kills1 ? kills2
• ins1 ins, ins2 ins
• outs outs1 U outs2

(a)
S
d a b c
S1
(b)
S
S2
(c)
S
S1
S2
12
DFA of Strongly Structured Programs (Cont)

• gens gens1
• kills kills1
• ins1 ins ? gens1
• outs outs1

(d)
S
S1

• Syntax directed definitions the equations are
  syntax directed.
• - synthesized attributes gen, kill, (out
  depends on in)
• - inherited attributes in ( in backward dir
  out)
• Note outs ? gens (gen definitions reaching
  end of S without
• following paths outside S)
• Loops Fixpoints Given gens, kills, ins
  we cannot simply
• use ins ins1. I J ? O
• ins1 ins ? outs1 O G ? ( I K)
• outs outs1 Take O0 ?
• outs1 gens1 ? (ins1 kills1) I1
  J1, O1 G ? ( J K)
• I2 J ? G, O2 O1