Data:

1
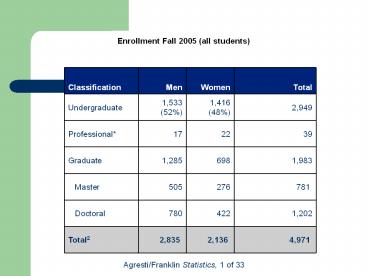
Enrollment Fall 2005 (all students)
2
Geographic Origin3 (Fall 2005)
3
Student Demographics (Fall 2005)
4
Chapter 1Statistics The Art and Science of
Learning from Data

• Learn .
• What Statistics Is
• Why Statistics Is Important

5
Chapter 1

• Learn
• How Data is Collected
• How Data is Used to Make
• Predictions

6
Section 1.1

• How Can You Investigate using Data?

7
Health Study

• Does a low-carbohydrate diet result in
  significant weight loss?

8
Market Analysis

• Are people more likely to stop at a Starbucks if
  theyve seen a recent TV advertisement for their
  coffee?

9
Heart Health

• Does regular aspirin intake reduce deaths from
  heart attacks?

10
Cancer Research

• Are smokers more likely than non-smokers to
  develop lung cancer?

11
To search for answers to these questions, we

• Design experiments
• Conduct surveys
• Gather data

12
Statistics is the art and science of

• Designing studies
• Analyzing data
• Translating data into knowledge and understanding
  of the world

13
Example from the National Opinion Center at the
University of Chicago

• General Social Survey (GSS) provides data about
  the American public
• Survey of about 2000 adult Americans

14
Example from GSS Do you believe in life after
death?
15
Three Main Aspects of Statistics

• Design
• Description
• Inference

16
Design

• How to conduct the experiment
• How to select the people for the survey

17
Description

• Summarize the raw data
• Present the data in a useful format

18
Inference

• Make decisions or predictions based on the data.

19
Example Harvard Medical School study of Aspirin
and Heart attacks

• Study participants were divided into two groups
• Group 1 assigned to take aspirin
• Group 2 assigned to take a placebo

20
Example Harvard Medical School study of Aspirin
and Heart attacks

• Results the percentage of each group that had
  heart attacks during the study
• 0.9 for those taking aspirin
• 1.7 for those taking placebo

21
Example Harvard Medical School study of Aspirin
and Heart attacks
Example Harvard Medical School study of Aspirin
and Heart attacks

• Can you conclude that it is beneficial for
  people to take aspiring regularly?

22
Section 1.2

• We Learn About Populations Using Samples

23
Subjects

• The entities that we measure in a study
• Subjects could be individuals, schools,
  countries, days,

24
Population and Sample

• Population All subjects of interest
• Sample Subset of the population for whom we have
  data

25
Geographic Origin (Fall 2005)
26
Enrollment Fall 2005
27
Majors (Fall 2005)
28
Example Format

• Picture the Scenario
• Question to Explore
• Think it Through
• Insight
• Practice the concept

29
Example The Sample and the Population for an
Exit Poll

• In California in 2003, a special election was
  held to consider whether Governor Gray Davis
  should be recalled from office.
• An exit poll sampled 3160 of the 8 million people
  who voted.

30

Example The Sample and the Population for an
Exit Poll
Example The Sample and the Population for an
Exit Poll

• Whats the sample and the population for this
  exit poll?
• The population was the 8 million people who voted
  in the election.
• The sample was the 3160 voters who were
  interviewed in the exit poll.

31
Descriptive Statistics

• Methods for summarizing data
• Summaries usually consist of graphs and numerical
  summaries of the data

32
Types of U.S. Households
33
Inference

• Methods of making decisions or predictions about
  a populations based on sample information.

34
Parameter and Statistic

• A parameter is a numerical summary of the
  population
• A statistic is a numerical summary of a sample
  taken from the population

35
Randomness

• Simple Random Sampling each subject in the
  population has the same chance of being included
  in that sample
• Randomness is crucial to experimentation

36
Variability

• Measurements vary from person to person
• Measurements vary from sample to sample

37
Inferential Statistics are used

• To describe whether a sample has more females or
  males.
• To reduce a data file to easily understood
  summaries.
• To make predictions about populations using
  sample data.
• To predict the sample data we will get when we
  know the population.

38
Chapter 2Exploring Data with Graphs and
Numerical Summaries

• Learn .
• The Different Types of Data
• The Use of Graphs to Describe
• Data
• The Numerical Methods of Summarizing Data

39
Section 2.1

• What are the Types of Data?

40
In Every Statistical Study

• Questions are posed
• Characteristics are observed

41
Characteristics are Variables

• A Variable is any characteristic that is
  recorded for subjects in the study

42
Variation in Data

• The terminology variable highlights the fact that
  data values vary.

43
Example Students in a Statistics Class

• Variables
• Age
• GPA
• Major
• Smoking Status

44
Data values are called observations

• Each observation can be
• Quantitative
• Categorical

45
Categorical Variable

• Each observation belongs to one of a set of
  categories
• Examples
• Gender (Male or Female)
• Religious Affiliation (Catholic, Jewish, )
• Place of residence (Apt, Condo, )
• Belief in Life After Death (Yes or No)

46
Quantitative Variable

• Observations take numerical values
• Examples
• Age
• Number of siblings
• Annual Income
• Number of years of education completed

47
Graphs and Numerical Summaries

• Describe the main features of a variable
• For Quantitative variables key features are
  center and spread
• For Categorical variables key feature is the
  percentage in each of the categories

48
Quantitative Variables

• Discrete Quantitative Variables
• and
• Continuous Quantitative Variables

49
Discrete

• A quantitative variable is discrete if its
  possible values form a set of separate numbers
  such as 0, 1, 2, 3,

50
Examples of discrete variables

• Number of pets in a household
• Number of children in a family
• Number of foreign languages spoken

51
Continuous

• A quantitative variable is continuous if its
  possible values form an interval

52
Examples of Continuous Variables

• Height
• Weight
• Age
• Amount of time it takes to complete an assignment

53
Frequency Table

• A method of organizing data
• Lists all possible values for a variable along
  with the number of observations for each value

54
Example Shark Attacks
55
Example Shark Attacks
Example Shark Attacks

• What is the variable?
• Is it categorical or quantitative?
• How is the proportion for Florida calculated?
• How is the for Florida calculated?

56
Example Shark Attacks

• Insights what the data tells us about shark
  attacks

57
Identify the following variable as categorical or
quantitative

• Choice of diet
• (vegetarian or non-vegetarian)
• Categorical
• Quantitative

58
Identify the following variable as categorical or
quantitative

• Number of people you have known who have been
  elected to political office
• Categorical
• Quantitative

59
Identify the following variable as discrete or
continuous

• The number of people in line at a box office to
  purchase theater tickets
• Continuous
• Discrete

60
Identify the following variable as discrete or
continuous

• The weight of a dog
• Continuous
• Discrete

61
Section 2.2

• How Can We Describe Data Using Graphical
  Summaries?

62
Graphs for Categorical Data

• Pie Chart A circle having a slice of pie for
  each category
• Bar Graph A graph that displays a vertical bar
  for each category

63
Example Sources of Electricity Use in the U.S.
and Canada
64
Pie Chart
65
Bar Chart
66
Pie Chart vs. Bar Chart

• Which graph do you prefer?
• Why?

67
Graphs for Quantitative Data

• Dot Plot shows a dot for each observation
• Stem-and-Leaf Plot portrays the individual
  observations
• Histogram uses bars to portray the data

68
Example Sodium and Sugar Amounts in Cereals
69
Dotplot for Sodium in Cereals

• Sodium Data
• 0 210 260 125 220 290 210 140
  220 200 125 170 250 150 170 70
  230 200 290 180

70
Stem-and-Leaf Plot for Sodium in Cereal

• Sodium Data 0 210
• 260 125
• 220 290
• 210 140
• 220 200
• 125 170
• 250 150
• 170 70
• 230 200
• 290 180

71
Frequency Table

• Sodium Data
• 0 210
• 260 125
• 220 290
• 210 140
• 220 200
• 125 170
• 250 150
• 170 70
• 230 200
• 290 180

72
Histogram for Sodium in Cereals
73
Which Graph?

• Dot-plot and stem-and-leaf plot
• More useful for small data sets
• Data values are retained
• Histogram
• More useful for large data sets
• Most compact display
• More flexibility in defining intervals

74
Shape of a Distribution

• Overall pattern
• Clusters?
• Outliers?
• Symmetric?
• Skewed?
• Unimodal?
• Bimodal?

75
Symmetric or Skewed ?
76
Example Hours of TV Watching
77

• Identify the minimum and maximum sugar values

78
Consider a data set containing IQ scores for the
general public

• What shape would you expect a histogram of this
  data set to have?
• Symmetric
• Skewed to the left
• Skewed to the right
• Bimodal

79
Consider a data set of the scores of students on
a very easy exam in which most score very well
but a few score very poorly

• What shape would you expect a histogram of this
  data set to have?
• Symmetric
• Skewed to the left
• Skewed to the right
• Bimodal