Multiple-key indexes

1
Multiple-key indexes

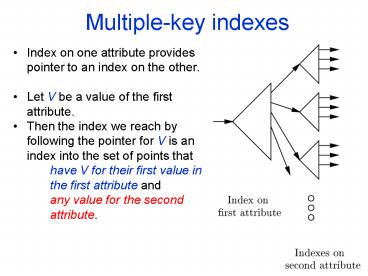
• Index on one attribute provides pointer to an
  index on the other.
• Let V be a value of the first attribute.
• Then the index we reach by following the pointer
  for V is an index into the set of points that
  have V for their first value in the first
  attribute and
• any value for the second attribute.

2
Example

• Who buys gold jewelry (age and salary only).
  Raw data in agesalary pairs
• (25 60) (45 60) (50 75) (50 100)
• (50 120) (70 110) (85 140) (30 260)
• (25 400) (45 350) (50 275) (60 260)
• Question For what kinds of queries will a
  multiplekey index (age first) significantly
  reduce the number of disk I/O's?

The indexes can be organized as B-Trees.
3
Operations

• Partial match queries
• If the first attribute is specified, then the
  access is quite efficient
• If the first attribute isnt specified, then we
  have to search every sub-index.
• Range queries
• Quite well, provided the individual indexes
  themselves support range queries on their
  attribute (e.g. they are B-Trees)
• Example. Range query is 35?age?55 AND 100?sal?200
• NN queries
• Similar to range queries.

Also, the indexes should be primary ones if we
want to support efficiently range queries.
4
KD-Trees

• Levels rotate among the dimensions, partitioning
  the points by comparison with a value for that
  dimension.
• Leaves are blocks holding the data records.

5
Geometrically

• Remember we didnt want the stripes in grid files
  to continue all along the vertical or horizontal
  direction?
• Here they dont.

6
Operations

• Lookup in KDTrees
• Find appropriate leaf by binary search. Is the
  record there?
• Insert Into KDTrees
• Lookup record to be inserted, reaching the
  appropriate leaf.
• If there is room, put record in that block.
• If not, find a suitable value for the appropriate
  dimension and split the leaf block using the
  appropriate dimension.
• Example
• Someone 35 years old with a salary of 500K buys
  gold jewelry.
• Belongs in leaf with (25 400) and (45 350).
• Too full split on age. See figure next.

7
Someone 35 years old with a salary of 500K buys
gold jewelry.
Its age turn to be used for split. Split at
35 its the median.
8
Queries

• Partial match queries
• When we dont know the value of the attribute at
  the node, we must explore both of its children.
• E.g. find points with age50
• Range Queries
• Sometimes a range will allow us to move to only
  one child of a node.
• But if the range straddles the splitting value
  then we must explore both children.

9
KD-trees in secondary storage

• If internal nodes dont fit in main memory group
  them into blocks.

10
Quad trees

• Nodes split at all dimensions at once
• For a quad tree of k dimensions, each interior
  node has 2k children.

11
Why quad trees?

• k-dimensions ? node has 2k children, e.g. k7 ?
  128 children.
• If 128, or 27, pointers can fit in a block, then
  k7 is a convenient number of dimensions.

12
QuadTree Insert and Queries

• Insert
• Find leaf node in which new point belongs.
• If room, put it there.
• If not, make the leaf an interior node and give
  it leaves for each quadrant. Split the points
  among the new leaves.
• Problem may make lots of null pointers,
  especially in highdimensions.
• QuadTree Queries
• Single point queries easy just go down the tree
  to proper leaf.
• Range queries varies by position of range.
• Example a range like 45ltagelt55 180ltsalarylt220
  requires search of four leaves.
• Nearest neighbor Problems and strategies similar
  to grid files.

13
R-Trees

• For regions (typically rectangles) but can
  represent points.
• Supports NN, whereamI queries.
• Generalizes Btree to multidimensional case.
• In place of Btree's keypointer pairs, Rtree
  has regionpointer pairs.

14
Lookup Where Am I?

• We start at the root, with which the entire
  region is associated.
• We examine the subregions at the root and
  determine which children correspond to interior
  regions that may contain point P.
• If there are zero regions we are done P is not
  in any data region.
• If there are some subregions we must recursively
  search those children as well, until we reach the
  leaves of the tree.

15
Insertion

• Inserting region R.
• 1. We start at the root and try to find some
  subregion into which R fits.
• If more than one we pick just one, and repeat the
  process there.
• 2. If there is no region, we expand, and we want
  to expand as little as possible.
• So, we pick the child that will be expanded as
  little as possible.
• 3. Eventually we reach a leaf, where we insert
  region R.
• 4. However, if there is no room we have to split
  the leaf.
• We split the leaf in such a way as to have the
  smallest subregions.

16
Example

• Suppose that the leaves have room for six
  regions.
• Further suppose that the six regions are together
  on one leaf, whose region is represented by the
  outer solid rectangle.
• Now suppose that another region POP is added.

17
Example (Cont ed)
((0,0),(60,50))
((20,20),(100,80))
Road1 Road2 House1
School House2 Pipeline Pop
18
Example (Cont ed)

• Suppose now that House3 ((70,5),(80,15)) gets
  added.
• We do have space to the leaves, but we need to
  expand one of the regions at the parent.
• We choose to expand the one which needs to be
  expanded the least.

19
Which one should we expand?
((0,0),(80,50))
((20,20),(100,80))
Road1 Road2 House1 House3
School House2 Pipeline Pop
Two choices
((0,0),(60,50))
((20,5),(100,80))
Road1 Road2 House1
School House2 Pipeline Pop House3
20
Bitmap Indexes

• Suppose we have n tuples.
• A bitmap index for a field F is a collection of
  bit vectors of length n, one for each possible
  value that may appear in the field F.
• The vector for value v has 1 in position i if the
  i-th record has v in field F, and it has 0 there
  if not.

(30, foo) (30, bar) (40, baz) (50, foo) (40,
bar) (30, baz)
foo 100100 bar 0 baz
21
Graphical Picture
Customer table. We will index Gender and Rating.
Note that this is just a partial list of all the
records in the table
Two bit strings for the Gender bitmap
Five bit strings for the Rating bitmap
Custid Name Gender Rating
112 Joe M 3
115 Sam M 5
119 Sue F 5
112 Wu M 4
1 2 3 4 5
0 0 1 0 0
0 0 0 0 1
0 0 0 0 1
0 0 0 1 0
M F
1 0
1 0
0 1
1 0
22
Bitmap operations

• Bit maps are designed to support partial match
  and range queries. How?
• To identify the records holding a random subset
  of the values from a given dimension, we can do a
  binary OR on the bitmaps from that dimension.
• For example, the OR of bit strings for Age (20,
  21, 22)
• To identify the partial matches on a group of
  dimensions, we can simply perform a binary AND on
  the ORd maps from each dimension.
• These operations can be done very quickly since
  binary operations are natively supported by the
  CPU.

23
Bit Map example
M F
1 0
1 0
0 1
1 0
1 2 3 4 5
0 0 1 0 0
0 0 0 0 1
0 0 0 0 1
0 0 0 1 0
SELECT FROM Customer WHERE gender M AND
(rating 3 OR rating 5)
24
Gold-Jewelry Data

• (25 60) (45 60) (50 75) (50 100)
• (50 120) (70 110) (85 140) (30 260)
• (25 400) (45 350) (50 275) (60 260)
• What would be
• the bitmap index for age, and
• the bitmap index for salary?
• Suppose we want to find the jewelry buyers with
  an age in the range 45-55 and a salary in the
  range 100-200. What do we do?

25
How big do these things get?

• Assuming each attribute value fits in a 32-bit
  machine word, the bitmap index for an attribute
  with value cardinality 32 takes as much space as
  the base data column.
• Since a B-tree index for a 32-bit attribute is
  often observed to use 3 or 4 times the space as
  the base data column, many users consider
  attributes with cardinalities less than 100 to be
  suitable for using bitmap indices.
• However, some other users believe bit map indexes
  are good for attributes with cardinalities more
  than 100. What can be done?

26
Basic Compression

• Run length encoding is used to encode sequences
  or runs of zeros.
• Say that we have 20 zeros, then a 1, then 30 more
  zeros, then another 1.
• Naively, we could encode this as the integer pair
  lt20, 30gt
• This would work. But what is the problem?
• On a typical 32-bit machine, an integer uses 32
  bits of storage. So our lt20, 30gt pair uses 64
  bits. The original string only had 52!
• So we must use a technique that stores our
  run-lengths as compactly as possible.
• Lets say we have the string 000101
• This is made up of runs with 3 zeros and 1 zero.
• In binary, 3 11, while 1 is, of course, just 1
• This gives us a compressed representation of 111.
• The problem?
• How do we decompress this?
• We could interpret this as 1-11 or 11-1 or even
  1-1-1.
• This would give us three different strings after
  the decompression.

27
Proper RLE encoding

• Run of length i has i 0s followed by a 1.
• So how does RLE store the run lengths?
• Lets say that that we have a run of length i.
• We set j the number of bits required to
  represent i.
• To define a run, we actually use two values
• The unary representation of j
• A sequence of j 1 1 bits followed by a zero
  (the zero signifies the end of the unary string)
• The special cases of j 0 and j 1 use 00 and
  01 respectively.
• The value i

28
Decoding

• Lets decode 11101101001011
• 11101101001011 ? 13
• 11101101001011 ? 0
• 11101101001011 ? 3
• Our sequence of run lengths is 13, 0, 3. Whats
  the bitmap?
• 0000000000000110001

29
Summary

• Pros
• Bitmaps provide efficient storage for low
  cardinality dimensions. On sparse, high
  cardinality dimensions, compression can be
  effective.
• Bit operations can support multi-dimensional
  partial match and range queries
• Cons
• De-compression requires run-time overhead
• Bit operations on large maps and with large
  dimension counts can be expensive.