Classic Async' Circuit Design

1
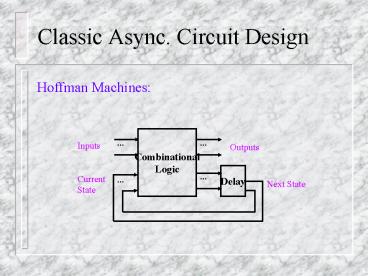
Classic Async. Circuit Design
Hoffman Machines
Combinational Logic
...
...
Inputs Current State
Outputs
Delay
...
...
Next State
2
Classic Async. Circuit Design

• Specification for Huffman Machines Flow Table
• Flow Table
• A. Two dimensional Array
• B. Columns input states
• C. Rows internal states
• D. Entry pair of Next state and Output
• E. N(s,i) Next internal state at current
  internal
• state s and current input state i.
• F. Z(s,i) Output at current internal state s
• and current input state i.
• G. Zk(s,i) The kth variable of Z(s,i)

3
Flow table C-element
Inputs A B Output C

• Total State input state internal state
• Stable total state current internal state
  next internal state

4
Flow table C-element

• Primitive Flow Tables
• A flow Table has at most one stable state per
  row.
• Non-primitive flow table 3 inputs, 2 outputs, 6
  states

5
Flow tablegt Circuits

• Goal Minimize the cost
• A. state minimization primitive FT gt reduced
  FT
• Flow table reduction a procedure to find
  minimal
• state flow table.
• B. state assignment assign each state (row) an
  code
• (state variables).
• R rows require at least log2R state variables.
• C. logic minimization produce gate level
  circuits
• for each state variables and outputs.

6
Flow tablegt Async. Circuits

• Beware of Async. Design
• A. state minimization
• Essential Hazards ??
• B. state assignment
• Race condition ??
• C. logic minimization produce
• Functional Combinational Hazards ??

7
State minimization

• State compatible
• two states i and j of a flow table is
  compatible
• if and only if for every possible input
  sequence
• applicable to i and j, the output sequences
  produced
• are the same at all positions where both are
  specified.
• State Incompatible if the output sequences
  differ,
• then i and j are incompatible.
• Ex states 1 and 2 are incompatible
• for Z2(1,010)0 and Z2(2,010)1

8
State minimization

• Conditional compatibles In some cases, for
• two states to be compatible, they require
  other states
• to be compatible too.
• Ex. the compatibility of states 3 and 5
• depends on states 4 and 5 being compatible.
• A set of states is a compatible if and only if
  every
• pair of states in the set are compatible.
• Ex. states 3, 4, and 5 are a compatible
  (named 345)
• because states 3 and 4, states 4 and 5,
  and
• states 3 and 5 are compatible.

9
State minimization

• Flow table and its Pair Chart

10
State minimization Compatibles
11
State minimization Compatibles

• A compatible Ci covers compatible Cj, (Ci gt Cj
  )
• if and only if Ci contains Cj.
• Ex. Compatible 345 gt compatible 34
• A maximal compatible is a compatible that is not
  
• covered by any other compatible.
• Ex. Compatible 345 is maximal but compatible
  34
• is not.

12
State minimization Compatibles
Ex. compatible 35 implies compatible 45 and
compatible 45 implies compatible 34 since
compatible 34 has no implications, the
closure class of compatible 35 is 45, 34.
13
Prime Compatibles
Ex. compatible 345 is prime but compatible 35 is
not, 1. compatible 35 is covered by
compatible 345 2. Closure class of 345 is
empty set and closure class of 35 is
45, 34.
14
Extended Closure Class
15
Closed Prime Compatibles

• A set of compatibles is closed if and only if,
  for
• every compatible contained in the set, each
  implied
• compatible is also contained in at least one
  compatible
• of the set. (the extended closure class is
  empty.)
• Ex. 1. the set of compatibles 34, 26 is
  closed.
• (Extended closure class of 34, 26 .)
• 2. the set 35, 26 is not.
• (Extended closure class of 35, 26 45,
  34.)

16
Minimal Covers (solutions)
Ex. 1, 26, 34, 5 and 1, 26, 345 are both
closed covers but the later is minimal and the
former is not.
17
Minimal Solutions
18
State Assignment

• State (row) Assignment Coding the internal
  state
• Goal A. No critical race condition
• the correctness depends on the race of
• state variables.
• B. Minimal number of state (binary-valued)
• variables

19
State Assignment

• Critical race the correctness depends on the
  outcome
• of the race

11 00 10
20
Logic Minimization

• Realize the output and state functions
• Output function Z
• State functions Y1 Y2

21
Essential Hazards

• Steady state essential hazards
• An incorrect stable state is reached when some
• input change.
• Transition essential hazards (output hazards)
• A glitch may appear on an output when some
• input change.
• Ex
• TEH (2,1) and x--gt0
• SSEH (1,0) and x--gt1