15'1 Linear Momentum and Impulse

1
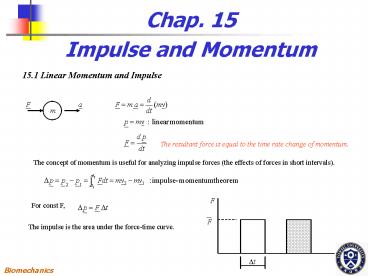
Chap. 15 Impulse and Momentum
15.1 Linear Momentum and Impulse
The resultant force is equal to the time rate
change of momentum.
The concept of momentum is useful for analyzing
impulse forces (the effects of forces in short
intervals).
For const F,
The impulse is the area under the force-time
curve.
2
15.2 Applications of the Impulse-Momentum Method

• Example

Conservation of energy
?
?
Linear momenta of the ball
?
?
Duration of collision
Impulse-momentum theorem
Average force by the floor on the ball during
collision?
3
Example 15.3 Vertical jumping on a force platform

• A force platform is a flat
• To measure the impulsive forces during jumping

Fig 15.3 A force platform

• The force vs. time recording shown in Fig.
  15.3(a)
• for an athlete making vertical jumps on a force
  
• platform.
• Determine an approximate take off velocity of the
• center of gravity of the athlete.
• Calculate the height of jump.
• Determine the impulse and momentum of the
• athlete during landing by using the
  approximated
• areas under the force versus time curve.

Fig 15.3(a)
4
Example 15.3 Vertical jumping on a force platform
(1) Take-off velocity of the athlete
(2) Height of jump
Using the conservation of energy,
(3) Impulse and momentum of the athlete during
landing
Fig 15.9 Normalized force versus time plot for
the athlete. (1 kN1000N)
5
15.2 Applications of the Impulse-Momentum Method

• Example A crash test

Initial horizontal speed
Time interval to rest
Average horizontal force by the dummy on the seat
belt?
But,
Impulse-momentum theorem
6
15.3 Conservation of Linear Momentum
Newtons 2nd law
When the system is in equilibrium, or the
resultant force is equal to zero,
Conservation of linear momentum

• Useful for impact and collision analysis

Let
By Newtons 3rd law,
Equilibrium condition
Whenever two objects collide, their total
momentum remains constant, regardless of the
nature of the forces between the two.
7
15.4 Impact and Collisions
Direct central impact
Oblique central impact

• Perfectly elastic collision Both the total
  momentum and total energy are conserved.
• Inelastic or plastic collision
• Only the total momentum is conserved.
• Some of kinetic energy is dissipated into heat.
• Perfectly plastic collision
• The objects stick together after the collision.
• Total momentum is always conserved.

8
15.5 1-D Collisions
Collision along a straight line (direct central
impact)
15.5.1 Perfectly inelastic collision
Before collision
After collision
1
1
2
2
Example
0
Thus, we have
9
15.5 1-D Collisions
15.5.2 Perfectly elastic collision
Before collision
After collision
1
1
2
2
Solving for
Example Billiard
Before collision
1
2
Before collision
1
2
10
15.5 1-D Collisions
15.5.3 Elasto-plastic collision

• In reality, elastic and plastic collision
• Coefficient of restitution, e

Approaching
Separation
1
1
2
2
e0 perfectly inelastic impact e1 perfectly
elastic impact

• Affecting factors of coefficient of restitution
• Material properties
• Temperature
• Relative approach velocity

11
15.5 1-D Collisions
15.6.3 Elasto-plastic collision
Example Bouncing Ball
(a) Coefficient of restitution?
?
?
Note
?
?
(b) Lost energy
Duration of collision
(a) Coefficient of restitution? (b) Lost energy?
12
15.6 Angular Impulse and Momentum
Translational motion
Rotational motion

• Linear Momentum

• Angular Momentum

• Angular Impulse-Momentum

• Linear Impulse-Momentum

• Force is the time rate of linear momentum.

• Moment is the time rate of angular momentum.

13
15.7 Summary of Basic Equations
Equations of Motion
Translational motion
Rotational motion
Velocity and Acceleration
Kinematic Relations for Const Acceleration
Equation of Motion
Work Done
Kinetic Energy
Work-Energy
Power
Momentum
Impulse-Momentum
14
15.8 Kinetics of Rigid Bodies in Plane Motion
Rigid bodies in Plane Motion

• Size and shape of the object do not affect the
  translation motion characteristics,
• But they affect the rotational motion
  characteristics.

For a rigid body in plane motion,
2-D general motion of the body (3 equations)
Newtons law of motion
The multi-force system can be reduced to a
one-force and one-moment system.