Priority Queues

1
Priority Queues
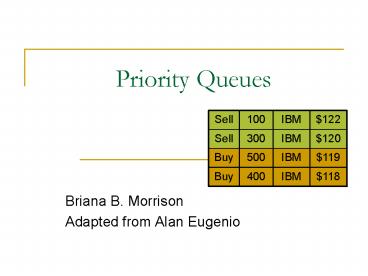
Sell 100 IBM 122
Sell 300 IBM 120
Buy 500 IBM 119
Buy 400 IBM 118

• Briana B. Morrison
• Adapted from Alan Eugenio

2
Topics

• API
• Application
• Implementation

3
Priority Queue
A Special form of queue from which items are
removed according to their designated priority
and not the order in which they entered.
Items entered the queue in sequential order but
will be removed in the order 2, 1, 4, 3.
4
A PRIORITY QUEUE IS A CONTAINER IN WHICH ACCESS
OR DELETION IS OF THE HIGHEST-PRIORITY
ITEM, ACCORDING TO SOME WAY OF ASSIGNING
PRIORITIES TO ITEMS.
5
(No Transcript)
6
(No Transcript)
7
(No Transcript)
8
(No Transcript)
9
(No Transcript)
10
(No Transcript)
11
(No Transcript)
12
(No Transcript)
13
(No Transcript)
14
(No Transcript)
15
(No Transcript)
16
(No Transcript)
17
(No Transcript)
18
(No Transcript)
19
(No Transcript)
20
(No Transcript)
21
(No Transcript)
22
(No Transcript)
23
(No Transcript)
24
void push(const T item) Insert the argument
item into the priority queue. Postcondition
The priority queue contains a new
element.
int size() const Return the number of items in
the priority queue.
T top() Return a reference to the item having
the highest priority. Precondition The
priority queue is not empty.
const T top() Constant version of top().
25
Comparator ADT

• A comparator encapsulates the action of comparing
  two objects according to a given total order
  relation
• A generic priority queue uses a comparator as a
  template argument, to define the comparison
  function (lt,,gt)
• The comparator is external to the keys being
  compared. Thus, the same objects can be sorted
  in different ways by using different comparators.
• When the priority queue needs to compare two
  keys, it uses its comparator

26
Using Comparators in C

• A comparator class overloads the () operator
  with a comparison function.
• Example Compare two points in the plane
  lexicographically.class LexCompare public
  int operator()(Point a, Point b) if
  (a.x lt b.x) return 1 else if (a.x gt
  b.x) return 1 else if (a.y lt b.y) return
  1 else if (a.y gt b.y) return 1
  else return 0

• To use the comparator, define an object of this
  type, and invoke it using its () operator
• Example of usagePoint p(2.3, 4.5)Point
  q(1.7, 7.3)LexCompare lexCompareif
  (lexCompare(p, q) lt 0) cout ltlt p less than
  qelse if (lexCompare(p, q) 0) cout ltlt
  p equals qelse if (lexCompare(p, q) gt 0)
  cout ltlt p greater than q

27
Applications

• Applications
• Standby flyers
• Auctions
• Stock market
• Sorting
• Huffman Coding

28
Sorting with a Priority Queue

• We can use a priority queue to sort a set of
  comparable elements
• Insert the elements one by one with a series of
  push(e) operations
• Remove the elements in sorted order with a series
  of pop() operations
• The running time of this sorting method depends
  on the priority queue implementation

• Algorithm PQ-Sort(S, C)
• Input sequence S, comparator C for the elements
  of S
• Output sequence S sorted in increasing order
  according to C
• P ? priority queue with comparator C
• while !S.empty ()
• e ? S.remove (S. first ())
• P.push(e)
• while !P.empty()
• e ? P.top() P.pop()
• S.insertLast(e)

29
(No Transcript)
30
(No Transcript)
31
(No Transcript)
32
(No Transcript)
33
(No Transcript)
34
(No Transcript)
35
(No Transcript)
36
(No Transcript)
37
(No Transcript)
38
(No Transcript)
39
(No Transcript)
40
(No Transcript)
41
(No Transcript)
42
(No Transcript)
43
(No Transcript)
44
(No Transcript)
45
(No Transcript)
46
(No Transcript)
47
(No Transcript)
48
(No Transcript)
49
(No Transcript)
50
Huffman Trees

• Problem Input A set of symbols, each with a
  frequency of occurrence.
• Desired output A Huffman tree giving a code that
  minimizes the bit length of strings consisting of
  those symbols with that frequency of occurrence.
• Strategy Starting with single-symbol trees,
  repeatedly combine the two lowest-frequency
  trees, giving one new tree of frequency sum of
  the two frequencies. Stop when we have a single
  tree.

51
Huffman Trees (2)

• Implementation approach
• Use a priority queue to find lowest frequency
  trees
• Use binary trees to represent the Huffman
  (de)coding trees
• Example b13, c22, d32 a64 e103
• Combine b and c bc35
• Combine d and bc d(bc)67
• Combine a and d(bc) a(d(bc))131
• Combine e and a(d(bc)) e(a(d(bc)))234 ... done

52
Huffman Tree Example
53
(No Transcript)
54
(No Transcript)
55
(No Transcript)
56
(No Transcript)
57
(No Transcript)
58
(No Transcript)
59
(No Transcript)
60
(No Transcript)
61
(No Transcript)
62
(No Transcript)
63
(No Transcript)
64
(No Transcript)
65
(No Transcript)
66
(No Transcript)
67
(No Transcript)
68
(No Transcript)
69
(No Transcript)
70
(No Transcript)
71
(No Transcript)
72
(No Transcript)
73
(No Transcript)
74
(No Transcript)
75
(No Transcript)
76
PQ Implementation

• How would you implement a priority queue?
• Several possibilities exist.

77
Sequence-based Priority Queue
Implementation 1
Implementation 2

• Implementation with an unsorted list
• Performance
• push takes O(1) time since we can insert the item
  at the beginning or end of the sequence
• pop, top take O(n) time since we have to traverse
  the entire sequence to find the smallest key

• Implementation with a sorted list
• Performance
• push takes O(n) time since we have to find the
  place where to insert the item
• pop, top take O(1) time since the smallest key is
  at the beginning of the sequence

78
Selection-Sort
Implementation 1 like sorting a hand of cards
(find smallest, next smallest)

• Selection-sort is the variation of PQ-sort where
  the priority queue is implemented with an
  unsorted sequence
• Running time of Selection-sort
• Inserting the elements into the priority queue
  with n push operations takes O(n) time
• Removing the elements in sorted order from the
  priority queue with n pop operations takes time
  proportional to 1 2 n
• Selection-sort runs in O(n2) time

79
Insertion-Sort
Implementation 2 like sorting a hand of cards
(put first in order, 2nd in order)

• Insertion-sort is the variation of PQ-sort where
  the priority queue is implemented with a sorted
  sequence
• Running time of Insertion-sort
• Inserting the elements into the priority queue
  with n push operations takes time proportional
  to 1 2 n
• Removing the elements in sorted order from the
  priority queue with a series of n pop operations
  takes O(n) time
• Insertion-sort runs in O(n2) time

80
In-place Insertion-sort

• Instead of using an external data structure, we
  can implement selection-sort and insertion-sort
  in-place
• A portion of the input sequence itself serves as
  the priority queue
• For in-place insertion-sort
• We keep sorted the initial portion of the
  sequence
• We can use swapElements instead of modifying the
  sequence

81
Summary Slide
- Priority queue - Pop() returns the highest
priority item (largest or smallest). - Norma
lly implemented by a heap, which is
discussed later in the class. - The
push() and pop() operations have running time
O(log2n)
81