Fly River, Papua New Guinea

1
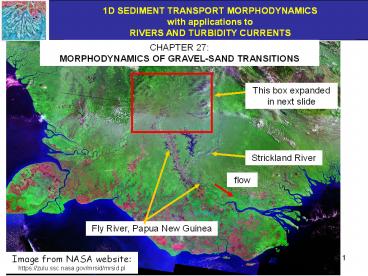
CHAPTER 27 MORPHODYNAMICS OF GRAVEL-SAND
TRANSITIONS
This box expanded in next slide
Strickland River
flow
Fly River, Papua New Guinea
Image from NASA website https//zulu.ssc.nasa.gov
/mrsid/mrsid.pl
2
THE BOX IS EXPANDED IN THE NEXT SLIDE TO SHOW A
GRAVEL-SAND TRANSITION
Ok Tedi
flow
flow
Fly River
Image from NASA website https//zulu.ssc.nasa.gov
/mrsid/mrsid.pl
3
GRAVEL-SAND TRANSITION ON THE OK TEDI, PAPUA NEW
GUINEA
flow
Wandering gravel-bed river
Gravel-sand transition
Meandering sand-bed river
flow
Image from NASA website https//zulu.ssc.nasa.gov
/mrsid/mrsid.pl
4
GRAVEL-SAND TRANSITION ON THE BENI RIVER, BOLIVIA
Image courtesy R. Aalto see Aalto (2002)
flow
Foredeep zone of tectonic susidence
Gravel-sand transition
Andes mountains zone of high tectonic uplift
flow
5
GRAVEL-SAND TRANSITION ON THE BENI RIVER, BOLIVIA
contd.
Note the discontinuity in grain size at the
gravel-sand transition.
Image courtesy R. Aalto see Aalto (2002)
flow
6
GRAVEL-SAND TRANSITION ON THE BENI RIVER, BOLIVIA
contd.
Note the discontinuity in slope at the
gravel-sand transition.
Image courtesy R. Aalto see Aalto (2002)
flow
7
GRAVEL-SAND TRANSITION KINU RIVER, JAPAN
Long profile showing downstream fining and
gravel-sand transition in the Kinu River, Japan
(Yatsu, 1955)
Both the gravel-bed and sand-bed reaches have
upward-concave profiles, and show downstream
fining. Note the sharp breaks in slope and grain
size! Sambrook-Smith and Ferguson (1995) have
documented many relatively sharp gravel-sand
transitions in rivers around the world.
8
SHARP GRAVEL-SAND TRANSITIONS ARE LIKELY
ASSOCIATED WITH A RELATIVE PAUCITY OF MATERIAL
IN THE RANGE 2-8 MM IN MANY RIVERS
This paucity was illustrated in Chapters 2 and 3.
It is common, but by no means universal.
From Chapter 3
From Chapter 2
9
THE SIMPLEST WAY TO MODEL LONG PROFILES WITH
GRAVEL-SAND TRANSITIONS IS TO CONSIDER A
TWO-GRAIN SYSTEM
The bed material of the gravel-bed reach is
characterized with a single size Dg. The bed
material of the sand-bed reach is characterized
with a single size Ds. The position of the
gravel-sand transition is x sgs. It is assumed
that the sand is transported through the
gravel-bed reach as wash load.
L reach length ?g elevation of gravel bed ?s
elevation of sand bed
10
SIMPLIFICATIONS OF THE PRESENT MODEL

• The model of this chapter focuses on gravel-sand
  transitions in subsiding basins, and in
  rivers-floodplain complexes subject to sea-level
  rise. The following simplifications are
  introduced.
• The gravel is characterized with a single grain
  size Dg, and the sand is characterized with a
  single grain size Ds. Grain size mixtures of
  gravel and sand are not considered.
• The total length of the gravel-bed reach plus
  the sand-bed reach the constant value L. The
  position of the gravel-sand transition x sgs(t)
  may change in time.
• No allowance is made for delta progradation.
• Abrasion of gravel to sand is neglected.
• It is assumed that there are no significant
  tributaries along the entire reach from x 0 to
  x L, so that water discharge during floods is
  constant downstream.
• Each reach (gravel-bed and sand-bed) is assumed
  to have a constant width.
• None of these assumptions would be overly
  difficult to relax.

11
PARAMETERS AND EXNER EQUATIONS

• x downchannel spatial coordinate L
• t time L
• g, ?s bed elevation on gravel-bed, sand-bed
  reach L
• qg, qs total volume gravel load, sand load per
  unit width L2/T
• ?pg, ?ps bed porosity of gravel-bed, sand-bed
  reach 1
• Ifg, Ifs flood intermittency on gravel-bed,
  sand bed reach 1
• ?g, ?s channel sinuosity on gravel-bed,
  sand-bed reach 1
• ?sg, ?ms volume fraction sand deposited per
  unit gravel, volume fraction mud deposited
• per unit sand in channel-floodplain complex 1
• rBg, rBs ratio of channel width Bc to
  depositional width Bd (basin or floodplain width)
  in
• gravel-bed, sand-bed reach (Bd,grav/Bc,grav or
  Bd,sand/Bc,sand)
• ? subsidence rate L/T

Based on the formulation of Chapter 25, the
conservation relations for gravel and sand on the
gravel-bed reach are The conservation relation
for sand on the sand-bed reach is
12
CONTINUITY CONDITION AT THE GRAVEL-SAND TRANSITION
Let ssg(t) denote the position of the gravel-sand
transition, and Sggs and Ssgs denote the gravel
bed slope and sand bed slope, respectively, at
the gravel-sand transition, so that
13
CONTINUITY CONDITION AT THE GRAVEL-SAND
TRANSITION contd.
In analogy to the treatment of bedrock-alluvial
transitions in Chapter 16, bed elevation
continuity at the gravel-sand transition is
expressed in the following form Taking the
derivate of both sides of the above equation with
respect to t and rearranging with the definitions
of Sggs and Ssgs of the previous slide, it is
found that
where dssg/dt denotes the migration speed
of the gravel-sand transition. Since gravel is
harder to move than sand, it can be expected that
Sggs gt Ssgs. Now suppose that near the
gravel-sand transition the sand-bed reach is
aggrading faster than the gravel-bed reach, i.e.
??s/?t gt ??g/?t. According to the above
equation, then, and the
gravel-sand transition migrates upstream.
14
THE LOCATION OF THE GRAVEL-SAND TRANSITION CAN
STABILIZE!
Consider a subsiding system that has reached a
steady state, as described in Chapter 26 In
such a case the continuity condition yields the
result i.e. an arrested gravel-sand
transition (Parker and Cui, 1998 Cui and Parker,
1998). If such a steady-state position exists,
the system will naturally evolve toward it. Sea
level rise at a constant rate can also lead
to an arrested gravel front when the following
condition is satisfied
15
MAXIMUM REACH LENGTH FOR STEADY STATE SYSTEM
In the case of a steady-state system entering a
basin subsiding at constant rate ? with constant
base level, the governing equations for the
gravel-bed reach reduce to and the governing
equation for the sand-bed reach reduces to The
corresponding forms for the case of a constant
rate of base level (sea level) rise in the
absence of subsidence are These forms are
closely allied to the steady-state forms
developed in Chapter 26.
Gravel-bed reach
Sand-bed reach
16
MAXIMUM REACH LENGTH FOR STEADY STATE SYSTEM
contd.
In general, then, the steady-state equations can
be written as where vv ? for the case of
constant subsidence without base level rise and
vv for the case of base level rise at a
constant rate without subsidence. Over the
gravel-bed reach, the top two equations integrate
to where qg,feed and qs,feed denote the
feed rates of sand and gravel (volume feed rate
per unit width) at x 0.
Gravel-bed reach
Sand-bed reach
Gravel and sand fill the accommodation space of
the gravel-bed reach created by subsidence or sea
level rise.
17
MAXIMUM REACH LENGTH FOR STEADY STATE SYSTEM
contd.
The gravel transport rate drops to zero (qg 0)
at the steady-state position of the gravel-sand
transition x ssg,ss given by the
relation The sand transport rate qs at the
point where the gravel runs out is Note that
in order for sand to be available for transport
beyond x Lgrav,max the following condition must
be satisfied The relation for the sand-bed
reach (second equation of previous slide) then
integrate to give
18
MAXIMUM REACH LENGTH FOR STEADY STATE SYSTEM
contd.
The sand transport rate drops to zero (qs 0) at
x Lmax, given by the relation or
thus If the reach length is longer than Lmax
it is not possible to reach a steady state which
maintains a specified base level at the
downstream end of the reach. This is because
there is not enough sediment (gravel and sand)
available to fill the accomodation space created
by subsidence or sea level rise. The result is
the formation of an embayment (drowned river
valley) at the downstream end.
19
REDUCTION OF THE CONTINUITY CONDITION TO A
RELATION FOR THE MIGRATION SPEED OF THE
GRAVEL-SAND TRANSITION
Returning to the non-steady-state problem, the
continuity condition reduces with the forms
for Exner of Slide 11, i.e. to yield the
following equation for the migration speed of the
gravel-sand transition
20
TRANSFORMATION TO MOVING BOUNDARY COORDINATES
The gravel-sand transition is free to move about
in time. It thus constitutes a moving boundary
problem. Moving boundary analysis was developed
in the context of a migrating bedrock-alluvial
transition in Chapter 16. Here it is adapted for
the case of a gravel-sand transition. Moving
boundary coordinates for the gravel-bed and
sand-bed reaches can be defined as Note that
on the gravel-bed reach, and
on the sand-bed reach. The Exner
equation for gravel conservation on the
gravel-bed reach of the previous slide transforms
to
21
TRANSFORMATION TO MOVING BOUNDARY COORDINATES
contd.
The Exner equation for the conservation of sand
on the gravel-bed reach, given in Slide 11,
transforms to The Exner equation for the
conservation of sand on the sand-bed reach, given
in Slide 15, transforms to The continuity
condition of Slide 12 describing the migration
speed of the gravel-sand transition transforms to
22
SPATIAL DISCRETIZATION
The spatial discretization involves MG gravel-bed
intervals followed by MS sand-bed intervals,
bounded by MG MS 1 nodes. The dimensionless
spatial steps for the gravel-bed and sand-bed
reaches are given as The node i MG MS 1
defines the downstream end of the reach, i.e. x
L. The node i MG 1 defines the gravel-sand
transition, i.e. x sgs. Gravel and sand are
fed in at a ghost node one step upstream of node
i 1.
23
CALCULATION OF FLOW
A backwater formulation is used to compute the
flow (which is assumed to be barely confined to
the channel). The friction coefficients on the
gravel-bed and sand-bed reaches, denoted
correspondingly as Cfg and Cfs, are assumed to be
specified constants. In accordance with Chapter
5, then, the backwater formulation for the
gravel-bed reach is where Hgrav denotes flow
depth on the gravel-bed reach, qw denotes the
water discharge per unit width (during floods)
and Sg denotes bed slope on the gravel-bed reach,
and the corresponding formulation for the
sand-bed reach is where Ss denotes the slope
and Hsand denotes the flow depth on the sand-bed
reach.
24
CALCULATION OF FLOW contd.
Transforming the relations of the previous page
to moving boundary coordinates results in the
forms
25
CALCULATION OF FLOW contd.
The boundary condition on the backwater
formulation is specified at x L, where
downstream water surface elevation ?d is
specified. Here may be a specified constant ?do
, or it may change in time at some constant rate
. Thus in general or In addition, a
continuity condition must be satisfied at the
gravel-sand transition
26
CALCULATION OF FLOW contd.
At any given time, the backwater curve above the
bed at that time can then be solved numerically
by implementing the formulation of Chapter 20
adapted to the present problem. That is, for the
sand-bed reach
27
CALCULATION OF FLOW contd.
The corresponding formulation for the gravel-bed
reach is
28
CALCULATION OF SHIELDS NUMBERS
The submerged specific gravity R ?s/? - 1 is
assumed to be the same for the gravel as it is
for the sand. Recall from Chapters 5 and 20 that
boundary shear stress ?b is given as where H
denotes flow depth, and that the Shields number
? is given as where D is an appropriate grain
size. Let U qw/H. The Shields number ?sand,i
at the ith node of the sand-bed reach is thus
given as and the corresponding value ?grav,i
for the ith node of the gravel-bed reach is given
as
29
CALCULATION OF SEDIMENT TRANSPORT
In the present implementation the gravel
transport on the gravel-bed reach is calculated
using the Parker (1979) approximation of the
Einstein (1950) relation introduced in Chapter 7
where qg denotes the volume gravel transport per
unit width and the subscript i denotes the ith
node, The sand transport on the sand-bed
reach is calculated using the Engelund-Hansen
(1967) formulation introduced in Chapter 12
where qs denotes the volume sand transport per
unit width and the subscript i denotes the ith
node,
30
CALCULATION OF BED EVOLUTION OF GRAVEL-BED REACH
The implementation of Exner on the gravel-bed
reach is as follows where qg,feed denotes the
volume feed rate per unit width of gravel at x
0,
31
CALCULATION OF CAPTURE OF SAND IN THE GRAVEL-BED
REACH
The model is designed so that washload (e.g. sand
for a gravel-bed stream) can be captured as the
gravel-bed channel aggrades over its depositional
width. This results in a downstream decrease in
qs over the gravel-bed reach, even though sand is
traveling as wash load. The decrease is
calculated by discretizing the following relation
from Slide 21 so yielding where qs,feed
denotes the volume feed rate per unit width of
sand at x 0.
32
CALCULATION OF BED EVOLUTION OF SAND-BED REACH
The implementation of Exner on the sand-bed reach
is as follows
33
CALCULATION OF MIGRATION OF GRAVEL-SAND TRANSITION
The migration speed of the gravel-sand transition
is given as This relation translates to the
following moving-boundary form where The
new position of the gravel-sand transition is
thus given as
34
INTRODUCTION TO RTe-bookGravelSandTransition.xls,
A CALCULATOR FOR THE EVOLUTION OF THE LONG
PROFILE OF A RIVER WITH A GRAVEL-SAND TRANSITION
THAT IS FREE TO MIGRATE
The analysis of the previous slides is
implemented in the workbook RTe-bookGravelSandTran
sition.xls. The code utilizes a large number of
input parameters in worksheet InData, as
enumerated below and on the next
slide Qbf bankfull discharge same for gravel-
and sand-bed reach L3/T Ifg flood
intermittency for gravel-bed reach 1 Ifs flood
intermittency for sand-bed reach
1 Qgrav,feed volume feed rate of gravel at x
0 (qg,feed Qgrav,feed/Bc,grav)
L3/T Qsand,feed volume feed rate of sand at x
0 (qs,feed Qsand,feed/Bc,sand)
L3/T Bc,grav bankfull width of gravel-bed
stream L Bc,sand bankfull width of sand-bed
stream L Bd,grav depositional width of
gravel-bed reach (rBg Bd,grav/Bc,grav)
L Bd,sand depositional width of sand-bed reach
(rBs Bd,sand/Bc,sand) L ?g sinuosity of
gravel-bed reach 1 ?s sinuosity of sand-bed
reach 1 ?sg volume fraction of sand deposited
per unit gravel in gravel-bed reach
1 ?ms volume fraction of mud deposited per unit
sand in sand-bed reach 1 Dg characteristic size
of gravel L Ds characteristic size of sand L
35
INTRODUCTION TO RTe-bookGravelSandTransition.xls
contd.
More input parameters specified in worksheet
InData of RTe-bookAgDegNormalGravMixSubPW.xls
are defined below. Czg Chezy resistance
coefficient of gravel-bed reach (Cfg Czg-2)
1 Czs Chezy resistance coefficient of sand-bed
reach (Cfs Czs-2) 1 L Reach length
L sgsI Initial value of distance sgs to
gravel-sand transition L SgI Initial slope of
gravel-bed reach 1 SsI Initial slope of
sand-bed reach 1 ? Subsidence rate
L/T ?do Initial value of sea level elevation
L rate of sea level rise L/T Yearstart Year
in which sea level rise starts T Yearstop Year
in which sea level rise stops T ?t Time step
T MG Number of gravel intervals MS Number of
sand intervals Mtoprint Number of time steps to
printout Mprint Number of printouts The following
parameters are specified in worksheet
AuxiliaryData porosity of deposit on
gravel-bed reach ?pg, porosity of deposit on
sand-bed reach ?ps and sediment submerged
specific gravity R (assumed to be the same for
sand and gravel).
36
NOTES AND CAVEATS

• The code locates the gravel-sand transition at a
  point determined by the continuity condition. At
  this point the gravel transport rate is only a
  small fraction of the feed value, but it is not
  precisely zero. In rivers, the small residual
  gravel load at gravel-sand transitions is either
  buried or consists of grains that easily break
  down to sand. In the code, the residual gravel
  load at the gravel-sand transition is added to
  the sand load.
• In the case of sea level rise at constant rate
  , rise can be commenced and halted at specified
  times Yearstart and Yearstop in worksheet
  InData.
• The reach length L should be chosen to be less
  than the maximum value Lmax, in order to ensure
  that there is enough sediment supply to fill the
  accomodation space created by subsidence or sea
  level rise. Guidance in this regard is provided
  in Cell C41 of worksheet InData.
• The initial downstream bed elevation is taken to
  be zero. As a result, the initial downstream
  water surface elevation ?do also equals the
  initial downstream depth. In order to ensure
  subcritical flow (and thus keep the calculation
  from crashing), ?do must be exceed the critical
  flow depth Hc (Qbf/Bc,sand)2/g-1/3. Guidance
  is provided in Cell C44 of worksheet InData.
• Depending on the input values, there may be no
  steady-state solution allowing a gravel-sand
  transition to equilibrate at a position between 0
  and L. For example, if 0 and ? 0, the
  only steady-state solution is one for which the
  sand is all driven into the sea. In such cases,
  the code will fail. (It would be an easy job to
  modify the code to handle such cases, but it has
  not been done). The code can be run, however, to
  a time at which the gravel-sand
• transition is nearly driven out of the
  domain of interest. Examples appear
• in succeeding slides.

37
EVOLUTION OF RIVER PROFILES WITH MIGRATING
GRAVEL-SAND TRANSITIONS CASE OF SEA LEVEL
RISE (WITH VANISHING SUBSIDENCE)
A parametric study is presented with rates of sea
level rise varying from 0 to 14 mm/year.
Input data for a base case ( 6 mm/year) are
given to the left and below.
38
d?/dt 0 mm/year
SEA LEVEL RISE OF 6 MM/YEAR FOR 6000 YEARS
Gravel-sand transition
39
d?/dt 0 mm/year
SEA LEVEL RISE OF 6 MM/YEAR FOR 6000 YEARS
Position of gravel-sand transition migrates
downstream and stabilizes as river aggrades.
40
d?/dt 0 mm/year
SEA LEVEL RISE OF 6 MM/YEAR FOR 6000 YEARS
The high slope near the gravel-sand transition is
an artifact of the calculation and should be
ignored see next slide.
Gravel-bed
Slope break at gravel-sand transition at steady
state
Sand-bed
41
d?/dt 0 mm/year
REASON FOR THE SPURIOUSLY HIGH GRAVEL-BED SLOPE
NEAR THE GRAVEL-SAND TRANSITION
In a backwater formulation, the actual continuity
condition is not the one given in Slide 13 in
terms of bed elevation but rather one expressed
in terms of water surface elevation Since ?
? H, this leads to the form
The extra terms would likely remove the spurious
slope, but would otherwise not change the
analysis much.
42
d?/dt 0 mm/year
SEA LEVEL RISE OF 6 MM/YEAR FOR 6000 YEARS
Sand load does not drop to zero even at steady
state
Sand
Gravel load drops nearly to zero at steady-state
gravel-sand transition
Gravel
43
SEA LEVEL RISE OF 6 MM/YEAR FOR 6000 YEARS
The gravel-sand transition migrates downstream
nearly to its steady state position within 2000
years.
44
SEA LEVEL RISE OF 0 MM/YEAR FOR 6000 YEARS
The model eventually fails shortly after 2160
years as the gravel-sand transition migrates
downstream out of the domain. This is to be
expected for a vanishing sea level rise.
45
SEA LEVEL RISE OF 2 MM/YEAR FOR 6000 YEARS
Again the gravel-sand transition migrates
downstream out of the domain, this time shortly
after 3780 years. The rate of sea level rise is
still not sufficient to stabilize the gravel-sand
transition within the domain.
46
SEA LEVEL RISE OF 3 MM/YEAR FOR 6000 YEARS
Gravel-sand transition location does not
stabilize by 6000 years, but neither does it
migrate downstream out of the domain.
47
SEA LEVEL RISE OF 4 MM/YEAR FOR 6000 YEARS
Gravel-sand transition migrates downstream and
starts to stabilize by 6000 years.
48
SEA LEVEL RISE OF 6 MM/YEAR FOR 6000 YEARS
Gravel-sand transition migrates downstream
modestly and stabilizes by 6000 years.
49
SEA LEVEL RISE OF 8 MM/YEAR FOR 6000 YEARS
Gravel-sand transition migrates slightly upstream
and stabilizes by 6000 years.
50
SEA LEVEL RISE OF 10 MM/YEAR FOR 6000 YEARS
Gravel-sand transition migrates supstantially
upstream and nearly stabilizes by 6000 years.
51
SEA LEVEL RISE OF 12 MM/YEAR FOR 6000 YEARS
Gravel-sand transition migrates even farther
upstream and nearly stabilizes by 6000 years.
52
SEA LEVEL RISE OF 14 MM/YEAR FOR 6000 YEARS
Rate of sea level rise is so large that there is
insufficient sediment to fill the accommodation
space. As a result, an embayment forms.
53
SEA LEVEL RISE OF 0 MM/YEAR UP TO YEAR 1000, 12
MM/YEAR FROM YEAR 1000 TO 4000, 0 MM/YEAR FROM
YEAR 4000 TO 6000
In this run Yearstart 1000 years and Yearstop
4000 years.
54
SEA LEVEL RISE OF 4 MM/YEAR UP TO YEAR 1000, 12
MM/YEAR FROM YEAR 1000 TO 4000, 4 MM/YEAR FROM
YEAR 4000 TO 6000
Note this calculation required changing 5 lines
of code.
Transition progrades out again
Transition moves upstream
Transition progrades out
55
EVOLUTION OF RIVER PROFILES WITH MIGRATING
GRAVEL-SAND TRANSITIONS CASE OF SUBSIDENCE (WITH
VANISHING SEA LEVEL RISE)
A reach with a length of 180,000 m and a
subsidence rate of 2 mm/year is considered. Two
cases are considered an initial position sgsI of
the gravel-sand transition of 15,000 m, and one
with an initial position of 60,000 m.
56
INITIAL POSITION OF THE GRAVEL-SAND TRANSITION
sgsI is 15,000 m
Subsidence rate ? 2 mm/year
Gravel-sand transition migrates downstream and
stabilizes by 12,000 years
57
INITIAL POSITION OF THE GRAVEL-SAND TRANSITION
sgsI is 15,000 m
Subsidence rate ? 2 mm/year
Gravel-bed
Sand-bed
58
INITIAL POSITION OF THE GRAVEL-SAND TRANSITION
sgsI is 15,000 m
Subsidence rate ? 2 mm/year
Sand
Gravel
59
INITIAL POSITION OF THE GRAVEL-SAND TRANSITION
sgsI is 15,000 m
Subsidence rate ? 2 mm/year
Gravel-sand transition migrates downstream and
stabilizes by 12,000 years
60
INITIAL POSITION OF THE GRAVEL-SAND TRANSITION
sgsI is 60,000 m
Subsidence rate ? 2 mm/year
Gravel-sand transition migrates upstream, but has
not quite stabilized by 48,000 years
61
INITIAL POSITION OF THE GRAVEL-SAND TRANSITION
sgsI is 60,000 m
Subsidence rate ? 2 mm/year
Gravel-bed
Sand-bed
62
INITIAL POSITION OF THE GRAVEL-SAND TRANSITION
sgsI is 60,000 m
Subsidence rate ? 2 mm/year
Sand
Gravel
63
INITIAL POSITION OF THE GRAVEL-SAND TRANSITION
sgsI is 60,000 m
Subsidence rate ? 2 mm/year
Gravel-sand transition migrates upstream, but has
not quite stabilized by 48,000 years
64
FURTHER COMMENTS

1. The model presented in this chapter allows
   neither downstream fining nor abrasion of gravel.
   Parker (1991a,b) provides a formulation of
   abrasion in the context of downstream fining of
   gravel-bed rivers, and Parker and Cui (1998) and
   Cui and Parker (1998) incorporate this
   formulation in a treatment of gravel-sand
   transitions.
2. Gravel-sand transitions have also been treated
   by Paola et al. (1992). In their treatment the
   location of the gravel-sand transition is
   determined by the point where the gravel runs out
   (gravel transport drops to zero).
3. Recent modeling work by Ferguson (2003) merits
   review by the interested reader.

65
REFERENCES FOR CHAPTER 27
Aalto, R., 2002, Geomorphic form and Process of
Sediment Flux within an Active Orogen Denudation
of the Bolivian Andes and Sediment Conveyance
across the Beni Foreland, PhD thesis, University
of Washington, USA, 365 p. Cui, Y. and Parker,
G., 1998, The arrested gravel front stable
gravel-sand transitions in rivers. Part 2
General numerical solution, Journal of Hydraulic
Research, 36(2) 159-182. Einstein, H. A., 1950,
The Bed-load Function for Sediment Transportation
in Open Channel Flows, Technical Bulletin 1026,
U.S. Dept. of the Army, Soil Conservation
Service. Engelund, F. and E. Hansen, 1967, A
Monograph on Sediment Transport in Alluvial
Streams, Technisk Vorlag, Copenhagen,
Denmark. Ferguson, R. I., 2003, Emergence of
abrupt gravel-sand transitions along rivers
through sorting processes, Geology 31,
159-162. Paola, C., Heller, P. L., and Angevine,
C. L., 1992, The large-scale dynamics of
grain-size variation in alluvial basins, 1
Theory, Basin Research, 4, 73-90. Parker, G.,
1979, Hydraulic geometry of active gravel rivers,
Journal of Hydraulic Engineering, 105(9),
1185-1201. Parker, G., 1991a, Selective sorting
and abrasion of river gravel theory, Journal of
Hydraulic Engineering, 117(2), 131-149. Parker,
G., 1991b, Selective sorting and abrasion of
river gravel applications, Journal of Hydraulic
Engineering, 117(2), 150-171. Parker, G., and Y.
Cui, 1998, The arrested gravel front stable
gravel-sand transitions in rivers. Part 1
Simplified analytical solution, Journal of
Hydraulic Research, 36(1) 75-100.
66
REFERENCES FOR CHAPTER 27 contd.
Sambrook Smith, G. H. and Ferguson, R., 1995, The
gravel-sand transition along river channels,
Journal of Sedimentary Research, A65(2)
423-430. Shaw, J. and R. Kellerhals, 1982, The
Composition of Recent Alluvial Gravels in Alberta
River Beds, Bulletin 41, Alberta Research
Council, Edmonton, Alberta, Canada. Yatsu, E.,
1955, On the longitudinal profile of the graded
river, Transactions, American Geophysical Union,
36 655-663.