Normal distribution

1
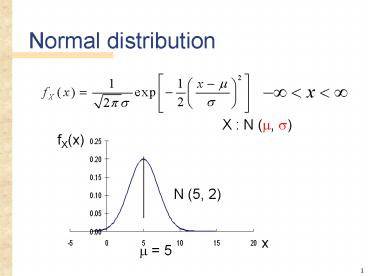
Normal distribution
X N (?, ?)
N (5, 2)
2
Effect of varying parameters (? ?)
fX(x)
? ? for C ? ? for B
B
C
A
x
3
Standard normal distribution
S N (0,1)
fX(x)
x
4
(No Transcript)
5
Page 380 Table of Standard Normal Probability
6
(No Transcript)
7
Given probability ?(a) p, ? a ?-1(p)
?
8
fX(x)
x
?
b
a
9
Example retaining wall
Suppose X N(200,30)
x
F
10
If the retaining wall is designed such that the
reliability against sliding is 99, How much
friction should be provided?
2.33
11
Lognormal distribution
Parameter l ?
12
Parameters ? ?
for ? ? 0.3,
13
Probability for Log-normal distribution
If a is xm, then ? is not needed.
14
P 3.19 Project completion time T
a)
Given information
T is normal
? 30
? ? 7.81
P (Tlt40) 0.9
15

• P (T lt 50)

b)
P ( T lt 0 )
Yes
Normal distribution ok?
16
c)
If assume Log-normal distribution for T, with
same value of m and s.
? 7.81/30 .26

• P (Tlt50)

17
P 3.20
Construction job that has a fleet of similar
equipments
In order to insure satisfactory operation, you
require at least 90 equipments available.
18
Each equipment has a breakdown time
T time until break down
Lognormal with mean 6 months, c.o.v. 25
19
0) Suppose scheduled time period for
maintenance is 5 months
P (an equipment will break down before 5 months)
P (Tlt5)
Expect 27 of equipment will not be operative
ahead of the next scheduled maintenance.
20
- Suppose need at least 90 equipment available
at any time
a)
- What should be the scheduled maintenance
period to?
P (breakdown of an equipment)
P (T lt to) ? 0.1
? to 4.22 months
21
b)
If to 4.22 months
P (will go for at least another month has
survived 4.22 months) ?
P (T gt 5.22 T gt 4.22)
0.6
0.749
22
Other distributions

• Exponential distribution
• Triangular distribution
• Uniform distribution
• Rayleigh distribution

p.224-225 table of common distribution
23
Exponential distribution
x ? 0
24
Example of application

• Quake magnitude
• Gap between cars
• Time of toll booth operative

25
Example
Given mean earthquake magnitude 5 in
Richter scale
P (next quake gt 7)
26
Shifted exponential distribution

• Lower bound not necessarily 0

x ? a
27
Beta distribution
q 2.0 r 6.0
probability
b 12
a 2.0
28
Standard beta PDF
(a 0, b 1)
fX(x)
q 1.0 r 4.0
q r 3.0
q 4.0 r 2.0
q r 1.0
x
29
Bernoulli sequence and binomial distribution

• Consider the bulldozer example
• If probability of operation p and start out
  with 3 bulldozers, what is the probability of a
  given number of bulldozers operative?

30
Let X no. of bulldozers operative
p?p?p
GGG GGB GBG BGG BBG BGB GBB BBB
3p?p?(1-p)
3p?(1-p)?(1-p)
(1-p)3
binomial coefficients
31
Suppose start out with 10 bulldozers
P (8 operative) P( X8 )
If p 0.9, then P (8 operative)
32
Bernoulli sequence
S
F
p probability of a success

• Discrete repeated trials
• 2 outcomes for each trial
• s.i. between trials
• Probability of occurrence same for all trials

33
Binomial distribution
S
F
x number of success
p probability of a success
P ( x success in n trials) P ( X x n, p)
34
Examples

• Number of flooded years
• Number of failed specimens
• Number of polluted days

35
Example
Given probability of flood each year 0.1
Over a 5 year period
P ( at most 1 flood year) P (X 0) P(X1)
0.95 0.328 0.919
36
P (flooding during 5 years) P (X ? 1) 1 P(
X 0) 1- 0.95 0.41
37
For binomial distribution
E (no. of success ) E(X) np
Over 10 years, expected number of years with
floods
E (X) 10 ? 0.1 1
38
P (first flood in 3rd year) ?
39
Geometric distribution
In general,
T time to first success
P (T t) (1-p)t-1p t1, 2,
geometric distribution
40
P (2nd flood in 3rd year)
P (1 flood in first 2 years)? P (flood in 3rd
year)
41
In general
P (kth flood in tth year)
P (k-1 floods in t-1 year)? P (flood in tth
year)
negative binomial distribution
42
Review of Bernoulli sequence

• No. of success ? binomial distribution
• Time to first success ? geometric distribution
• E(T) 1/p return period

43
Significance of return period in design
Service life
Suppose ?? expected to last 100 years and if it
is designed against 100 year-wind of 68.6 m/s
design return period
P (exceedence of 68.6 m/s each year) 1/100
0.01
P (exceedence of 68.6 m/s in 100th year) 0.01
44
P (1st exceedence of 68.6 m/s in 100th year)
0.9999?0.01 0.0037
P (no exceedence of 68.6 m/s within a service
life of 100 years) 0.99100 0.366
P (no exceedence of 68.6 m/s within the return
period of design) 0.366
45
If it is designed against a 200 year-wind of 70.6
m/s
P (exceedence of 70.6 m/s each year) 1/200
0.005
P (1st exceedence of 70.6 m/s in 100th year)
0.99599?0.005 0.003
46
P (no exceedence of 70.6 m/s within a service
life of 100 years) 0.995100 0.606 gt 0.366
P (no exceedence of 70.6 m/s within return period
of design) 0.995200 0.367
47
How to determine the design wind speed for a
given return period?

• Get histogram of annual max. wind velocity
• Fit probability model
• Calculate wind speed for a design return period

48
Frequency
Example
Annual max wind velocity
Design for return period of 100 years p 1/100
0.01
?V100 90.6 mph
49
Alternative design criteria 1
Suppose we design it for 100 mph, what is the
corresponding return period?
50
Probability of failure
Pf P (exceedence within 100 years) 1- P (no
exceedence within 100 years) 1- (1-0.000233)100
0.023
51
Alternative design criteria 2
If P (exceedence within the life time of the
building, i.e., 100 years) 0.01
Q What should be the design wind velocity?
Let T design return period
?P (annual exceedence) 1/T
P (no exceedence in 100 year) (1-1/T)100 1-
0.01
52
? T 10000 year
?VD 101.76 mph
53
P 3.28
A preliminary planning study on the design of a
bridge over a river recommended an acceptable
probability of 30 of the bridge being inundated
by flood in the next 25 years
a) p probability of exceedence in one year ?
P (exceedence of design flood within 25 years)
0.3
Hence, 1- P(no exceedence in 25 years) 0.3
? p 0.0142
54
b ) what is the return period for the
design flood?
Return period of design flood T 1/p 1/0.0142
70.4 year
55
Review of Bernoulli sequence model

• x success in n trials binomial
• time to first success geometric
• time to kth success negative binomial

56
Suppose average rate of left turns is n 1.5
/min
Q P (8 LTs in 6 min) ?
Mean number of occurrence in 6 min 9
(a) 6 min divided into 30 second interval
? No. of interval 12
57
(b) 6 min divided into 10 second interval
? No. of interval 36
(c) In general,
P ( 8 occurrences in n trials)
No. of occurrences in time interval nt
58
P ( x occurrences in n trials)
x 0, 1, 2,
Poisson distribution
59
e.g. x 8, t 6 min n 1.5 per min
P (2 LTs in 30 sec) P(X 2)
60
P (at least 2 LTs in 1 min) P(X?2) 1-
P(X0)-P(X1)
61
Poisson Process

1. An event can occur at random and at any time or
   any point in the space
2. Occurrence of an event in a given interval is
   independent of any other nonoverlapping intervals.

62
Example
Mean rate of rainstorm is 4 per year
P (2 rainstorms in next 6 months)
P (at least 2 rainstorms in next 6 months)
P(X?2) 1- P(X0)-P(X1)
63
Design of length of left-turn bay
Suppose LTs follow a Poisson process
100 LTs per hour
How long should LT bay be?
Assume all cars have the same length Let the bay
be measured in terms of no. of car length k
Suppose traffic signal cycle 1 min Cars waiting
for LT will be clear at each cycle
64
If k 0 ,ok 19 of time
If k 1 , ok 50
If k 2 , ok 76
If k 3 , ok 91
If k 4 , ok 97
65
Suppose criteria is adequate 96 of time
? k 4
In general,
k ?
If criteria changes, k changes
66
Mean of Poisson r.v. nt Variance of Poisson
r.v. nt
?c.o.v.
67
P 3.42
Service stations along highway are located
according to a Poisson process Average of 1
station in 10 miles ? n 0.1 /mile
P(no gasoline available in a service station)
68
No. of service stations
(a)
P( X ? 1 in 15 miles ) ?
69
(b) P( none of the next 3 stations have
gasoline)
No. of stations with gasoline
binomial
70
(c) A driver noticed the fuel gauge reads empty
he can go another 15 miles from experience.
P (stranded on highway without gasoline) ?
No. of station in 15 miles
P (S)
71
x P( S X x ) P( X x ) P( S X x ) P( X x )
0 1 e-1.5 0.223 0.223
1 0.2 1.5 e-1.5 0.335 0.067
2 0.22 1.52/2! e-1.5 0.251 0.010
3 0.23 1.53/3! e-1.5 0.126 0.001
4 0.24 1.54/4! e-1.5 0.047 0.00007
Total 0.301
72
Alternative approach
Mean rate of service station 0.1 per
mile Probability of gas at a station 0.8 ?
Mean rate of wet station 0.1?0.8 0.08 per
mile
Occurrence of wet station is also Poisson
?P (S) P ( no wet station in 15 mile)
73
P 3.48
Consider reliability of a tower over next 20 years
74
The tower can withstand an earthquake whose
magnitude is 5 or lower
Damaging earthquake ? magnitude gt 5
75
P (tower subjected to less than 3 damaging
earthquakes during its lifetime) ?
a)
from record
76
Lift-time reliability
b) P ( tower will not be destroyed by
earthquakes within its useful life) ?
77
c) tower also subjected to tornadoes
If a tornado hits tower, the tower will be
destoryed.
tower damaged by tornadoes
78
P (tower damaged by natural hazards)
79
Time to next occurrence in Poisson process
Time to next occurrence T is a continuous r.v.
P (X 0 in time t)
Recall for an exponential distribution
80
?T follows an exponential distribution with
parameter l n
? E(T) 1/n
If n 0.1 per year, E(T) 10 years
81
Example
Storms occurs according to Poisson process with n
4 per year 1/3 per month
P ( next storm occurs between 6 to 9 months from
now)
82
Comparison of two families of occurrence models
Bernoulli Sequence Poisson Process
Interval Discrete Continuous
No. of occurrence Binomial Poisson
Time to next occurrence Geometric Exponential
Time to kth occurrence Negative binomial Gamma
83
Multiple Random Variables
E 3.24
Duration and productivity (x,y) No. of observations Relative frequencies
6, 50 2 0.014
6, 70 5 0.036
6, 90 10 0.072
8, 50 5 0.036
8, 70 30 0.216
8, 90 25 0.180
10, 50 8 0.058
10, 70 25 0.180
10, 90 11 0.079
12, 50 10 0.072
12, 70 6 0.043
12, 90 2 0.014
Total 139
84
Joint PMF PX,Y (x,y)
PX,Y (x,y)
y
0.079
0.4
0.014
90
0.3
70
0.2
0.014
50
0.1
x
0.0
12
10
6
8
PX,Y(6,50) 0.014
P(Xgt8,Ygt70) 0.0790.014 0.093
85
Marginal PMF PY(y), PX(x)
PY(y)
PX,Y (x,y)
y
0.180
0.216
0.432
0.4
90
0.317
0.3
70
0.036
0.2
50
0.129
0.122
0.1
PX(x)
x
0.0
12
10
6
8
P(X8) 0.0360.2160.180 0.432
86
Conditional PMF
P(Y70 X8) PYX(70 8)
87
If X and Y are s.i.
or
88
Joint and marginal PDF of continuous R.V.s
marginal PDF fX (x)
marginal PDF fY (y)
xa
fX (a) Area
fX,Y (x, yb)
Surface fX,Y (x,y)
y b
Joint PDF
fY (b) Area
fX,Y (xa, y)
89
a) Calculate probability
90
b) Derive marginal distribution
91
c) Conditional distribution
92
Correlation coefficient a measure of correlation
between X and Y
93
Significance of correlation coefficient
r 1.0
r -1.0
94
r 0
0lt r lt1.0
95
Estimation of r from data
96
Review of Chapter 3

• Random variables
• discrete PMF, CDF
• continuous PDF, CDF
• Main descriptors
• central values mean, median, mode
• dispersion variance, s, c.o.v.
• skewness
• Expected value of function

97

• Common continuous distribution
• normal, lognormal, exponential
• Occurrence models
• Bernoulli sequence binomial, geometric,
  negative binomial
• Poisson process Possion, exponential, gamma

98

• Multiple random variables
• Discrete joint PMF, CDF, marginal PMF,
  conditional PMF
• Continuous joint PDF, marginal PDF, conditional
  PDF
• Correlation coefficient