Cumulus

1
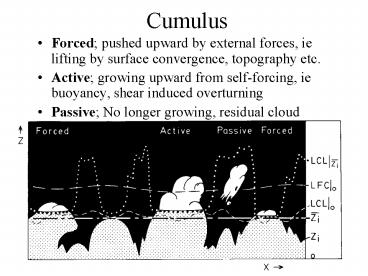
Cumulus

• Forced pushed upward by external forces, ie
  lifting by surface convergence, topography etc.
• Active growing upward from self-forcing, ie
  buoyancy, shear induced overturning
• Passive No longer growing, residual cloud

2
Cumulus Clouds

• Shallow Cumulus (cumulus, scatted cumulus,
  strato-cumulus)
• Depth small compared to scale height of
  troposphere, i.e.
• Usually confined to Planetary Boundary Layer
  (PBL)
• Typically non-precipitating
• Surface friction plays critical role to
  organization
• Deep Cumulus (congestus, cumulonimbi)
• Depth comparable to scale height of troposphere
• Precipitating
• Friction plays secondary role to organization

3
Instabilities Resulting in Cumulus

• Three basic atmospheric flow instabilities
• Inertial Instability Against horizontal inertial
  balance, i.e. horizontal pressure gradient,
  coriolis and centrifugal force
• Static Instability (absolute instability)
  Against vertical hydrostatic balance, i.e.
  vertical pressure gradient and gravity force
• Symmetric Instability Against inertial balance
  on an isentropic (constant potential temperature)
  surface, i.e. isentropic pressure gradient force,
  coriolis and isentropic centrifugal force (a
  combination of 1 and 2! Think about this!)

4
Symmetric Instability
5
Static Instabilities

• Conditional, i.e. only if saturated
• (CI) Conditional (static) instability
• (CSI) Conditional Symmetric Instability
• Frictional, ie in the PBL
• Rayleigh- Bernard
• Inflection Point Instability
• (KH) Kelvin-Helmholtz
• Gravity Wave Resonance

6
Kelvin-Helmholtz Instability

• Small perturbation tends to amplify by the
  advection of vorticity (shear gt curvature)
• Resistance to growth of wave by static stability,
  
• ie Brunt-Vasallai Frequence, N
• Condition for instability

7
(No Transcript)
8
(No Transcript)
9
Rayleigh-Benard Instability

• Results when a thin layer of fluid is subjected
  to to heat fluxes from to or bottom of layer
• Forces
• Promoting overturning heat flux
• Resisting overturning friction

10
Rayleigh Number

• Non-dimensional number depicting ratio of heat
  flux or buoyancy forcing to frictional
  resistance
• h is fluid depth (m)
• is the lapse rate (K/m)
• is the coefficient of expansion
• D is the viscosity (m2/s)
• K is the thermal conductivity (K m/s)

11
Condition for Rayleigh-Benard Instability

• Linearize Navier stokes equations
• Assume wave solution
• Then the condition for instability is

12
Condition for Rayleigh-Benard Instability
(continued)

• Instability for any number of combinations of k
  and l including
• Cells
• Rolls
• The value that Ra must exceed is a function of
  horizontal wave number

13
Most Unstable Rayleigh-Benard Mode

• Differentiate stability condition w.r.t.
  horizontal wave number and set to zero to obtain
  condition for maximum (growth rate)
• If for simplicity we assume and
  we assume square cells
  where S is the spacing, then a ratio of
  horizontal spacing to depth Sh31 is implied.

14
Hexagonal form to Rayleigh Benard Convection
15
Organization of Boundary Layer Convection

• Cellular (Rayleigh-Benard)
• Closed Cells
• Open Cells
• Linear
• Wind Parallel (Rayleigh-Benard)
• Inflection Point (Kelvin-Helmholtz)
• Gravity Wave Resonance
• Spoked (Rayleigh-Benard)
• Actinae

16
Cellular Convection
17
Mesoscale Cellular Convection (MCC)
18
Linear Convection
19
Open, Closed and Actinae Convection
20
Linear,Roll-type Convection
21
Hexagonal Cells
22
Cellular Convection

• Also known as mesoscale Cellular Convection (MCC)
• Two types
• Type I typically to the east of continents
  during the winter season over warm ocean currents
  (driven by heating from below)
• Type II Occur during the summer to the west of
  continents over cool ocean currents (driven by
  cooling from above)

23
(No Transcript)
24
Cellular Convection

• Open vs. closed cells
• Wintertime cold air masses that advect from
  continents out over warm ocean currents produce
  convective marine PBLs. 
• Cold air masses that advect from continents out
  over warm ocean currents produce convective
  marine PBLs. 
• The convective cloudiness that evolves off-shore
  occurs as bands or streets and gives way
  downstream to chains  of open cells and then
  farther out to sea there are eventually  patterns
  of open and closed hexagonal convection

25
Cellular Convection

• Open vs. closed cells
• This is the   natural order to expect as unstable
  convective PBLs are growing and near steady-state
  can develop in time with sufficient heating (and
  farther out to sea, which also finds the
  decreasing effects of vertical shear in the
  horizontal wind (lt10-3s-1)          

26
Cellular Convection

• Actinae spoke-like cellular convection formations
• Actinae do not occur in Type I CTBLs, because the
  process  is too dynamic. 
• Actinae only occur in Type II CTBLs.  The reason
  being that in the Rayleigh-Prandtl regime
  stability  diagram there is a very small space (a
  narrow range of conditions that will support
  actinae). 
• In the Type II case the atmosphere is functioning
  in such a slow dynamic mode that the  actinae can
  be achieved.  It is easy to produce the actinae
  in the laboratory. 

27
Cellular Convection

• Actinae spoke-like cellular convection formations
• The spoke-pattern convection is a geometric
  plan-form that represents a transition between
  the open and  closed cellular convection
  patterns.  It is a transitional pattern and that
  is why it is always found between regions of 
  open and closed cells. 
• In thermal convection (both theory and  lab
  results) you can develop 6-arm patterns (linear
  mode for  weakly supercritical Rayleigh) to
  12-arm patterns (non-linear mode). 
• Rotation would be no surprise because background
  vertical vorticity gets stretched  and the
  convective overturning (especially during
  transition           from open to closed
  structure) produces horizontal vortex tubes  as
  well. 

28
Actinae