References

1
(No Transcript)
2
(No Transcript)
3
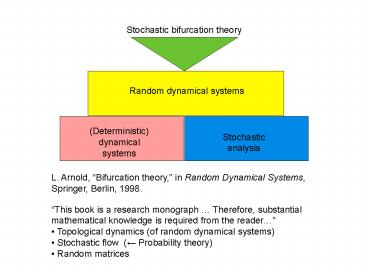
References

• L. Arnold, Bifurcation theory, in Random
  Dynamical Systems, Springer, Berlin, 1998, Chap.
  9.
• L. Arnold, Toward an understanding of stochastic
  Hopf bifurcation A case study, International J.
  Bif. Chaos, Vol. 6 1947-1975, 1996.
• L. Arnold, Stochastic bifurcation instructive
  exmples in dimension one, in Diffusion Process
  and Related Problems in Analysis, V. II,
  Stochastic Flow (Eds., M. A. Pinsky and V.
  Wihstutz), pp. 241-256.

4

• Background
• Random dynamical systems
• (Stochastic bifurcations)
• 2.1 P-bifurcation
• 2.2 D-bifurcation
• Case studies
• 3.1 Dimension one
• 3.2 Dimension two

5
The Word Bifurcation

• The word bifurcation, meaning some sort of
  branching process, is widely used to describe any
  situations in which the quantitative, topological
  picture of the object we are studying alters with
  a change of the parameters on which the objects
  depends. The objects in question can be extremely
  diverse for example, real or complex curves or
  surface functions or maps, manifolds or
  fibrations, vector fields, differential or
  integral equations.
• 
  Vladimir Igorevich Arnold

6
Bifurcation theory
(Deterministic) bifurcation theory
Bifurcation ?
qualitative changes in the phase portrait of
parameterized family of dynamical systems

• topological equivalence
• structural stability

Stochastic bifurcation theory ?

• Phenomenological approach (stationary densities)
• Dynamical approach

7
Stochastic differential equation and stationary
densities
A family of stochastic differential equations
(SDEs)
drift
diffusion coefficient
Stationary probability densities
Fokker-Plank equation
Notice
In general there are several different SDEs with
the same associated p(x).
8
Stochastic differential equation and stationary
densities
Example 1
For t in T and, X T? ? ?, the SDE dXt dWt
gives X(t x)x Wt. Letting Y(t x) X(t x)
mod 2p, this gives a diffusion on the unit sphere
S1 with generator the operator We then get the
Lebesgue measure on S1 as the unique stationary
measure.
Example 2
Let (Wt1) and (Wt2) be independent
one-dimensional Wiener processes. The SDE dXt
sinXt dWt1cosXt dWt2 is 2p-periodic in the
initial conditions, therefore it can be
interpreted as a SDE on S1. Then, the generator
is
9
Phenomenological approach (P-bifurcation)
Equivalent densities (p ? q)
Two densities p and q are said to be equivalent
(p ? q) if there are diffeomorphisms ?1 and ?2
such that Then, p ? q implies that the number
of local maxima and minima of p and q are equal
(Zeeman, 1988).
Definition of P-bifurcation
The value ?0 is a bifurcation point if in every
neighborhood of ?0 there are non-equivalent
invariant densities p?1, p?2. This is called a
phenomenological or P-bifurcation (Arnold, 1998
Crauel, 2003).
10
Phenomenological approach (P-bifurcation)
Some remarks on P-bifurcation

• Advantage of P-bifurcation it only needs to know
  stationary densities, not the random dynamical
  systems.
• Disadvantage it is not scale invariant, i.e.,
  if X is a random variable whose distribution has
  two maxima, there is a strictly monotone
  transformation h ??? such that ?(h(X)) the low
  of random variable X on ? has only one maximum.

Example
Let X be a real random variable with
Two peaks
For h ???
monotone transformation
We get
Then
One peak
11
Push-forward vs. pullback
Langevin equation
General solution
Push-forward (cf. non-autonomous systems)
stochastic process
Pullback (cf. autonomous systems)
random variable
12
Dynamical systems vs. random dynamical systems
13
D-bifurcation
Definition of D-bifurcation (Arnold et al., 1996)
Given a family (??) , for ? in ?, of random
dynamical systems, assume ?? has an invariant
measure ?? (reference measure) . Then (?0, ??0
) is called a dynamical, or D-bifurcation
point if for each ? in a neighborhood of ?0,
there is a ??-invariant measure ?? ??? for which
?? ???0 weakly as ? ??0 .
Theorem (Arnold and Xu, 1994)
Let (??) be a family of random dynamical systems
with ??(t,?)00 (i.e., with reference measure
???0) . Let ?0 a D-bifurcation point. If ?? ? ?0
(? ??0) then necessarily one Lyapunov exponent
vanishes.
14
4. Case studies Dimension one, two, and more
15
Dimension one - Transcritical bifurcation

• Analysis of D-bifurcations
• Invariant measures
• Solutions of SDEs (or RDEs)
• Lyapunov exponents
• Bifurcation points
• Variational (linearized) equations
• Stable/unstable subspaces

16
Dimension one - Transcritical bifurcation
(Deterministic) Differential Equation
Bifurcation diagram
steady state
stable
a
unstable
17
Dimension one - Transcritical bifurcation
Trivial solution
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
18
Dimension one - Transcritical bifurcation
Invariant measures (stationary solutions)
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
19
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
20
Dimension one - Transcritical bifurcation
1. Case alt 0
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
21
Dimension one - Transcritical bifurcation
1. Case alt 0
A. stochastic stable subspace (manifold)
Exponentially fast
B. stochastic unstable subspace
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
22
Dimension one - Transcritical bifurcation
2. Case agt 0
(i)
3. Case a0
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
23
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
24
Dimension one - Transcritical bifurcation
Summary of D-bifurcation
Invariant measure
D-bifurcation bifurcation point
25
Dimension one - Transcritical bifurcation

• Analysis of P-bifurcations
• Fokker-Plank (FP) equation
• Stationary distributions
• (invariant measures)
• P-bifurcation points

26
One-dimensional SDE and the FP equation
General theory
27
Dimension one - Transcritical bifurcation
Stochastic Differential Equation (SDE)
FP equation
Stationary probability density
(i)
(ii)
(Arnold, 1998, pp. 477-480)
28
Dimension one - Transcritical bifurcation
P-bifurcation
Stationary probability densities
pdf
altap
P-bifurcation point
aap
agtap
x
Parameters (s,ap)(2,2)
P-bifurcation point
29
Dimension one - Transcritical bifurcation
Summary of D- and P-bifurcation
30
(No Transcript)
31
Dimension one - Pitchfork bifurcation
Invariant measures
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
32
Dimension one - Pitchfork bifurcation
Linearization (variational equation) of the SDE
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
33
Dimension one - Pitchfork bifurcation
1. Case alt 0
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
34
Dimension one - Pitchfork bifurcation
35
Dimension one - Pitchfork bifurcation
3. Case a0
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
36
(No Transcript)
37
Dimension one - Pitchfork bifurcation
Summary of D-bifurcation
38
Dimension one - Pitchfork bifurcation

• Analysis of P-bifurcations
• Fokker-Plank (FP) equation
• Stationary densities
• (invariant measures)
• P-bifurcation points

39
Dimension one - Pitchfork bifurcation
Stochastic Differential Equation (SDE)
FP equation
(Arnold, 1998, pp. 477-480)
40
Dimension one - Pitchfork bifurcation
Stationary probability densities
41
Dimension one - Pitchfork bifurcation
Summary of P-bifurcation
42
Dimension one - Pitchfork bifurcation
Summary of D- and P-bifurcations
P-bifurcation
D-bifurcation
D-bifurcation point
P-bifurcation point
Each bifurcation point is different!
43
steady state
stable
a
unstable
44
Dimension one - Saddle-node bifurcation
(undamped random linear oscillator)
(Arnold and Boxler, 1992Arnold, 1998, pp.
477-480)
45
Dimension one - Saddle-node bifurcation
White noise case
(cf. trace formula)
i.e., if the noise is Gaussian, the undamped
random linear oscillator is unstable
(Arnold, Kliemann, and Oeljeklaus, in Lyapunov
Exponents, 1984)
After the white Gaussian-noise perturbation, the
saddle-node bifurcation disappears. The noise
destroys the bifurcation!
Real (bounded) noise case The destruction
could be avoided in some real noise cases.
(cf., Arnold et al., 1984 Arnold, 1998, p. 490)
46
Dimension one - Saddle-node bifurcation
Stochastic Differential Equation (SDE)
FP equation
Stationary probability density
(Arnold, 1998, pp. 477-480)
47
(No Transcript)
48
Dimension two
Stochastic Duffing-van der Pol (DVDP) Oscillator
Deterministic case (i.e.,s0)
For alt 0, ß24alt0 and the bifurcation parameter
ß, a Hopf bifurcation occurs at ß0. Two
complex-conjugate eigenvalues
49
Bifurcation diagram for the stochastic DVDP
oscillator alt0, s?0
50
P-bifurcation for the stochastic DVDP oscillator
Stationary probability densities
Fokker-Plank equation
51
Stochastic Duffing-van der Pol Oscillator
P-bifurcation
b-0.3
b-0.03
b0
b0.03
b0.3
b2.0
(Arnold et al., 1998)
52
(No Transcript)
53
D-bifurcation analysis for the DVDP oscillator

• General Analysis of D-bifurcations
• First step
• Find
• invariant measures,
• Lyapunov exponents
• stable/unstable subspaces
• However, if we cannot find explicitly
• Second step
• Approximation
• asymptotic method
• stochastic averaging
• Stochastic normal forms (Arnold, 1998, Chap. 8)

54
Linearization of the Stochastic DVDP Oscillator
Linearization
Variational equation
Trace formula
55
D-bifurcation analysis for the DVDP oscillator

• General Analysis of D-bifurcations
• First step
• Find
• invariant measures,
• Lyapunov exponents
• stable/unstable subspaces
• However, if we cannot find explicitly
• Second step
• Approximation
• asymptotic method
• stochastic averaging
• Stochastic normal forms (Arnold, 1998, Chap. 8)

56
Asymptotic method Small noise expansion of
Lyapunov Exponent (LE) Complex eigenvalues case
(Arnold et al., 1998, p. 499)
57
Small noise expansion of LEs for the Stochastic
DVDP Oscillator
Using a linear translation
we obtain the following equation
(Arnold, 1996)
58
Bifurcation scenario of D-bifurcation for the
stochastic DVDP oscillator (a-1, s?1)
2
2
(Arnold et al., 1996)
59
D-bifurcation analysis for the DVDP oscillator

• General Analysis of D-bifurcations
• First step
• Find
• invariant measures,
• Lyapunov exponents
• stable/unstable subspaces
• However, if we cannot find explicitly
• Second step
• Approximation
• asymptotic method
• stochastic averaging
• Stochastic normal forms (Arnold, 1998, Chap. 8)

60
Averaging principle deterministic case (Freidlin
and Wentzell, 1984, Chap. 7)
Approximation
61
Averaging principle stochastic case (Freidlin
and Wentzell, 1984, Chap. 7)
Approximation
62
Stochastic averaging method
Average stochastic SDE (Khasminskii, 1966)
Trivial solution u0 (the origin) ? Trivial
invariant measure d0
(Khasminskii, 1966 Arnold et al., 1996)
63
Stochastic averaging technique for the
Stochastic DVDP Oscillator
Average SDE in the polar coordinate
Trivial solution r0 (the origin) ? Trivial
invariant measure d0
(Khasminskii, 1966 Arnold et al., 1996)
64
P-bifurcation of the stochastic averaged DVDP
Oscillator
The first equation is decoupled i.e.,
Pitchfork bifurcation
Therefore,
In contrast,
Hence,
65
P-bifurcation diagram for stochastic DVDP
oscillator (a-1, s?1)
Stationary densities
creator
pole at zero
Dirac
P-bifurcation point
66
Stability of the trivial measure
Variational (linearized) equation
Solutions
Lyapunov exponents
Rotation number
67
Averaged equations
Original
Linearized
Deterministic equation
original
linearized
Lyapunov exponent
Tangent space at u
68
Lyapunov exponent
original
linearized
Invariant measure for ?
Solutions
Ergodic theorem (cf. Stationary density is
known.)
Lyapunov exponent
69
Oseledets splitting of the tangent space of the
averaged system at the base point
u-plane
v-plane
70
Summary for the averaged DVDP oscillator
(1) invariant measure d0
D-bifurcation point
(2) invariant measure
71
Bifurcation diagram for the averaged DVDP (s gt 0)
1. Stationary densities
2. Invariant measures
3. Lyapunov exponents
72
Bifurcation diagram for the stochastic DVDP
oscillator alt0, s?0
P-bifurcation
crater
Dirac
pole at zero
D-bifurcation
(Arnold et al., 1998)
73
t0
t3
Discrete Lebesgue measure 100100 points
t15
t100
d0 stable
74
t5
t10
t100
t10000
?1 stable
75
t5
t20
t100
t1000
d0 saddle
?1 stable
76
t3
t7
t300
t1000
?1 stable
d0 unstable
77
Some other examples Application of random
dynamical systems

• Physical systems
• Lorenz equation (Sri Namachchivaya, 1990 Keller,
  1996)
• Duffing-van der Pol oscillator (Arnold et al,
  1996)
• Brusselator (Lefever and Turner, 1984, 1986
  Arnold et al., 1998)
• Kramers oscillator (Arnold and Imkeller, 1998)
• Dumped harmonic oscillator (Imkeller and Lederer,
  1999)
• Hamiltonian systems (Arnold et al., 2001)
• Neural models
• Hodgkin-Huxley model (Pakdaman and Tanabe, 2001)
• FitzHugh-Nagumo model (Kosmidis and Pakdaman,
  2003)
• Morris-Lecar model (Tateno and Pakdaman, 2004)

78
Support of for the noisy
Duffing-van der Pol equation (a-1, ß0.002,s0.5)
100100 points
1
-1
-1
1
(Arnold et al., 1996)
79
100100 points
t0
t12
t25
1
-1
-1
1
t35
t50
t100
(Arnold et al., 1996)
80
Domain of attraction of µ? and attractor for a-1
ands0.5.
ß0.02
ß0.5
1
-1
-1
1
(Arnold et al., 1996)
81
Stationary densities of the normal form (a-1,
s0.5)
ß-0.01
ß-0.1
ß0.01
ß0.1
(Arnold et al., 1996)
82
Bifurcation diagram for the noisy Duffing-van der
Pol osciilator alt0, s?0
d0 unstable ? saddle µ stable
d0 saddle µ stable
d0 stable
(Arnold et al., 1996)
83
Stationary measures for the noisy Duffing-van der
Pol equation (a-1, s1)
ß1
ß-1
ß0
(Arnold et al., 1996)
84
(Arnold et al., 1998)