Introducci

1
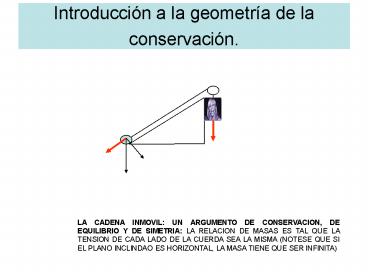
Introducción a la geometría de la conservación.
LA CADENA INMOVIL UN ARGUMENTO DE CONSERVACION,
DE EQUILIBRIO Y DE SIMETRIA LA RELACION DE MASAS
ES TAL QUE LA TENSION DE CADA LADO DE LA CUERDA
SEA LA MISMA (NOTESE QUE SI EL PLANO INCLINDAO ES
HORIZONTAL, LA MASA TIENE QUE SER INFINITA)
2
Un problema clásico de conservación
Reversibilidad de las maquinas y el equilibrio
permanente.
LA CADENA INMOVIL UN ARGUMENTO DE CONSERVACION,
DE EQUILIBRIO Y DE SIMETRIA Un argumento de
conservación, la energía del sistema tiene que
ser constante. Al mover la cuerda, la energia de
La Pradon cambia en la misma cantidad que se ha
desplazado la cuerda (mgh), y la de la masa en
una cantidad menor (mgh/sen(a))
3
El problema clásico de conservación regla de
tres.
3
5
Cuál es la relación entre m1 y m2 si se esta en
equilibrio?
4
El argumento de Stevins Conservacion de energia
y equlibrio
LA CADENA INMOVIL UN ARGUMENTO DE CONSERVACION,
DE EQUILIBRIO Y DE SIMETRIA.
5
Fuerza, desplazamiento, trabajo y esfuerzo.
La cantidad relevante es la proyección de la
fuerza sobre el eje de desplazamiento. Cuanto mas
ortogonales son la dirección de la fuerza y del
movimiento, esta proyección es menos importante y
por lo tanto la fuerza tiene que aumentar en
magnitud. Nótese que el problema en la otra
dirección (normal al plano) esta resuelto
trivialmente por la solidez del plano.
Igualmente, el cambio de energía en esta versión
integral del problema incorpora la relación
angular entre la fuerza y el desplazamiento. El
cambio de energía es proporcional a la proyección
del desplazamiento EN LA DIRECCION en que actúa
la fuerza.
6
Diferencial de energía en varias (dos)
dimensiones. La integral de la fuerza a lo largo
de su dirección.
7
Diferencial de energía en varias (dos)
dimensiones. La integral de la fuerza a lo largo
de su dirección.
8
Diferencial de energía en varias (dos)
dimensiones. La integral de la fuerza a lo largo
de su dirección.
9
Diferencial de energía en varias (dos)
dimensiones. La integral de la fuerza a lo largo
de su dirección.
10
Diferencial de energía en varias (dos)
dimensiones. La integral de la fuerza a lo largo
de su dirección.
O aun reordenando términos
Diferencial de Trabajo (por definición) y aquí se
adivina la relevancia de esta cantidad.
Diferencial de Energía Cinetica
11
Diferencial de energía en varias (dos)
dimensiones. La integral de la fuerza a lo largo
de su dirección.
En general se puede resolver el problema en la
dirección de movimiento. Esto es trivial (ha de
hacerse una sola vez) cuando el movimiento es
rectilíneo, independientemente de la dirección de
la fuerzs. Cuando el movimiento es curvo el
problema es iterativo porque para hacer esta
proyección hace falta conocer la trayectoria para
la cual hace falta conocer las fuerzas y así
siguiendo
La proyección de la fuerza que contribuye al
trabajo (y de hecho, en este caso, al movimiento)
porque el plano ejerce una fuerza igual y
contraria con lo que todas la fuerzas resultante
son paralelas a la dirección de movimiento. En un
caso genérico, fuerzas transversales pueden
contribuir al movimiento (modificando la
dirección, sin realizar trabajo)
12
Primer manifestación de la direccionalidad El
signo
Un campo de fuerzas constante
Trayectoria forzada en un campo constante Cuál
es el trabajo de esta fuerza?
(x1,v1)
(x2,v2)
13
Primer manifestación de la direccionalidad El
signo
Un campo de fuerzas constante
Trayectoria forzada en un campo constante Cuál
es el trabajo de esta fuerza?
(x1,v1)
(x2,v2)
14
Mapas Escalares La anatomía de la función
abs(xy)
A lo largo de curvas
En coordenadas polares
Imagenes del mapa
15
Gradiente, la dirección (y cantidad de cambio, de
una función escalar)
16
Mapas Escalares La anatomía de la función
xexp(r2)
Dos representaciones equivalentes de las ternas
(x,y,f(x,y))
Las curvas de nivel, o las direcciones a lo largo
de las cuales una función no cambia y aquellas,
ortogonales, de máximo cambio.
17
Inferir la tendencia al cambio a partir de una
función potencial
18
Inferir la tendencia al cambio a partir de una
función potencial
Función Potencial y campo gradiente, dos
conceptos hermanaos. El gradiente es el vector
formado por el valor de cambio (con signo) en
cada dirección. Apunta entonces en la dirección
donde la función mas crece. La fuerza es inversa
al gradiente y cambia el momento (alterando la
tendencia a mantener la velocidad constante).
Nótese que el momento evoluciona en dirección de
los pozos de potencial. Nótese también que el
movimiento no converge a los pozos (es decir, no
se estaciona en un mínimo) porque la partícula
tiene inercia. Un pozo suficientemente profundo
atrapa una particula que oscila en este pozo.