System and definitions

1
System and definitions
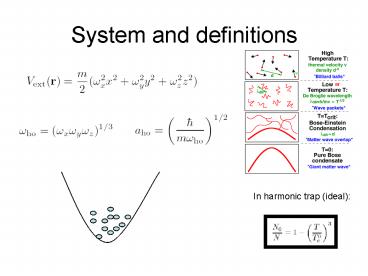
er
In harmonic trap (ideal)
2
Dilute interacting Bosons
Single particle field operators
Macroscopic occupation assumption
Homogeneous result
3
Dilute interacting Bosons
an operator!
Not an operator!
Inhomogeneous (time and space)
Single particle density matrix formalism
Time evolution of operator in Heisenberg Rep.
Scattering theory (see ahead)
Mean-field assumption discard fluctuating part
Time-Dependent Gross- Pitaevskii equation (TDGPE)
4
A short review of scat. theory
Eigenvalue scattering problem
Fourier Trans.
Born Approx.
Low k limit (s-wave)
Indistinguishable particles
Effective potential!
5
GPE ground state properties
Variational derivation Energy functional
Smallness parameter
Interaction energy
Kinetic energy
Weak interactions ? ideal gas behavior!
(still small depletion, but strongly non-ideal)
6
GPE ground state properties
TDGPE
Ansatz normalization
TIGPE
Note energy is not a good quantum number
(nonlinear problem!)
7
Numerical solution of TDGPE
Imaginary time evolution
Interacting ground-state
Non-interacting ground-state
(Mean-field repulsion causes increase in Size)
8
Thomas-Fermi approx.
Neglect kinetic term
Relaxed
T.F.
9
Excitations Bogoliubov equations
Ansatz (plug Into TDGPE)
Neglect terms of order u2, v2 and uv
Bogoliubov equations (linearized GPE)
Homogeneous system (u(r) and v(r) are plane
waves)
10
Homogeneous Bogoliubov spectrum
Interaction vs. Quantum
Pressure
healing length
11
Bragg Spectroscopy
M. Kozuma, et. al., PRL 82, 871 (1999). J.
Stenger, et. al., PRL 82, 4569 (1999).
12
The Measured Excitation Spectrum
(using Bragg spectroscopy)
Liquid Helium (scaled for comparison)
13
Phonon Region
14
Superfluidity!
Landau criteria
Interactions lead to superfluidity!
Superfluid velocity
A few mm/sec in experimental systems!
15
Many body theory (homogeneous)
Assume macroscopic occupation of S.P. Ground
state
Put in assumption keep terms of order
and
The number operator is conserved can be placed
in
16
Many body theory (homogeneous)
Neglected
Bogoliubov Transform
Atomic commutation relations give
17
Many body theory (homogeneous)
Eliminate off-diagonal third line
Convenient representation
Solution of quasi-particle amplitudes
18
Diagonalized Hamiltonian
Energy spectrum (again)
Ground state is a highly non-trivial Superposition
of all momentum states
Ground state energy
19
Quasi-particle physics
Inverse transformation
Particle creation
Particle Annihilation
Quasi-particle factors for repulsive condensates
Low k limit
High k limit
20
Quasi-particle physics
???
Dont Forget Bosonic Enhancement!
21
Quantum depletion of S.P. ground state
Evaluate the non-single-particle component of the
ground state at T0
About 1 for standard experiments
22
Attractive collapse!
Complex energy unstable to excitation!
Finite size can save us (cutoff in Low ks)
Experimental values A few thousand atoms!
23
Structure factor and Feynman relation
Static structure factor (Fourier transform of the
density-density correlation function)
T0
24
Static Structure Factor

• Measure of
• Response at k
• Fluctuations with wave-number k

25
Excitation Spectrum of Superfluid 4He
D. G. Henshaw and A. D. B. Woods, Phys. Rev. 121,
1266 (1961).
D. G. Henshaw, Phys. Rev. 119, 9 (1960).
26
Higher order Beliaev and Landau damping
Akq The many-body suppression factor
Beliaev
k-q
k
q
q
27
Damping rate
Fermi golden rule
28
Damping rate
Excitations
Impurities
29
Points not covered
- Inhomogeneous Bogoliubov theory - Beyond T0 -
Coherent collisions of excitations (FWM) -
Hydrodynamic representation of GPE - Na3 1
theory and experiment