Comparing k > 2 Groups - Numeric Responses

1
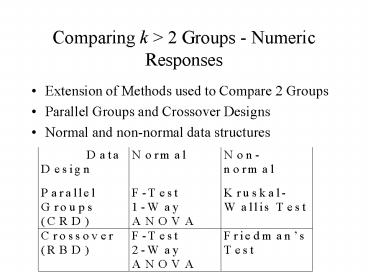
Comparing k gt 2 Groups - Numeric Responses

• Extension of Methods used to Compare 2 Groups
• Parallel Groups and Crossover Designs
• Normal and non-normal data structures

2
Parallel Groups - Completely Randomized Design
(CRD)

• Controlled Experiments - Subjects assigned at
  random to one of the k treatments to be compared
• Observational Studies - Subjects are sampled from
  k existing groups
• Statistical model Yij is a subject from group i

where m is the overall mean, ai is the effect of
treatment i , eij is a random error, and mi is
the population mean for group i
3
1-Way ANOVA for Normal Data (CRD)

• For each group obtain the mean, standard
  deviation, and sample size

• Obtain the overall mean and sample size

4
Analysis of Variance - Sums of Squares

• Total Variation

• Between Group Variation

• Within Group Variation

5
Analysis of Variance Table and F-Test

• H0 No differences among Group Means
  (a1???ak0)
• HA Group means are not all equal (Not all ai
  are 0)

6
Example - Relaxation Music in Patient-Controlled
Sedation in Colonoscopy

• Three Conditions (Treatments)
• Music and Self-sedation (i 1)
• Self-Sedation Only (i 2)
• Music alone (i 3)
• Outcomes
• Patient satisfaction score (all 3 conditions)
• Amount of self-controlled dose (conditions 1 and
  2)

Source Lee, et al (2002)
7
Example - Relaxation Music in Patient-Controlled
Sedation in Colonoscopy

• Summary Statistics and Sums of Squares
  Calculations

8
Example - Relaxation Music in Patient-Controlled
Sedation in Colonoscopy

• Analysis of Variance and F-Test for Treatment
  effects

• H0 No differences among Group Means
  (a1???a30)
• HA Group means are not all equal (Not all ai
  are 0)

9
Post-hoc Comparisons of Treatments

• If differences in group means are determined from
  the F-test, researchers want to compare pairs of
  groups. Three popular methods include
• Dunnetts Method - Compare active treatments with
  a control group. Consists of k-1 comparisons, and
  utilizes a special table.
• Bonferronis Method - Adjusts individual
  comparison error rates so that all conclusions
  will be correct at desired confidence/significance
  level. Any number of comparisons can be made.
• Tukeys Method - Specifically compares all
  k(k-1)/2 pairs of groups. Utilizes a special
  table.

10
Bonferronis Method (Most General)

• Wish to make C comparisons of pairs of groups
  with simultaneous confidence intervals or 2-sided
  tests
• Want the overall confidence level for all
  intervals to be correct to be 95 or the
  overall type I error rate for all tests to be
  0.05
• For confidence intervals, construct
  (1-(0.05/C))100 CIs for the difference in each
  pair of group means (wider than 95 CIs)
• Conduct each test at a0.05/C significance level
  (rejection region cut-offs more extreme than when
  a0.05)

11
Bonferronis Method (Most General)

• Simultaneous CIs for pairs of group means

• If entire interval is positive, conclude mi gt mj
• If entire interval is negative, conclude mi lt mj
• If interval contains 0, cannot conclude mi ? mj

12
Example - Relaxation Music in Patient-Controlled
Sedation in Colonoscopy

• C3 comparisons 1 vs 2, 1 vs 3, 2 vs 3. Want
  all intervals to contain true difference with 95
  confidence
• Will construct (1-(0.05/3))100 98.33 CIs for
  differences among pairs of group means

Note all intervals contain 0, but first is very
close to 0 at lower end
13
CRD with Non-Normal Data Kruskal-Wallis Test

• Extension of Wilcoxon Rank-Sum Test to kgt2 Groups
• Procedure
• Rank the observations across groups from smallest
  (1) to largest (n n1...nk), adjusting for
  ties
• Compute the rank sums for each group T1,...,Tk .
  Note that T1...Tk n(n1)/2

14
Kruskal-Wallis Test

• H0 The k population distributions are identical
  (m1...mk)
• HA Not all k distributions are identical (Not
  all mi are equal)

Post-hoc comparisons of pairs of groups can be
made by pairwise application of rank-sum test
with Bonferroni adjustment
15
Example - Thalidomide for Weight Gain in HIV-1
Patients with and without TB

• k4 Groups, n1n2n3n48 patients per group
  (n32)
• Group 1 TB patients assigned Thalidomide
• Group 2 TB- patients assigned Thalidomide
• Group 3 TB patients assigned Placebo
• Group 4 TB- patients assigned Placebo
• Response - 21 day weight gains (kg) -- Negative
  values are weight losses

Source Klausner, et al (1996)
16
Example - Thalidomide for Weight Gain in HIV-1
Patients with and without TB
17
Weight Gain Example - SPSS OutputF-Test and
Post-Hoc Comparisons
18
Weight Gain Example - SPSS OutputF-Test and
Post-Hoc Comparisons
19
Weight Gain Example - SPSS OutputKruskal-Wallis
H-Test
20
Crossover Designs Randomized Block Design (RBD)

• k gt 2 Treatments (groups) to be compared
• b individuals receive each treatment (preferably
  in random order). Subjects are called Blocks.
• Outcome when Treatment i is assigned to Subject j
  is labeled Yij
• Effect of Trt i is labeled ai
• Effect of Subject j is labeled bj
• Random error term is labeled eij

21
Crossover Designs - RBD

• Model

• Test for differences among treatment effects
• H0 a1 ... ak 0 (m1 ... mk )
• HA Not all ai 0 (Not all mi are equal)

22
RBD - ANOVA F-Test (Normal Data)

• Data Structure (k Treatments, b Subjects)
• Mean for Treatment i
• Mean for Subject (Block) j
• Overall Mean
• Overall sample size n bk
• ANOVATreatment, Block, and Error Sums of
  Squares

23
RBD - ANOVA F-Test (Normal Data)

• ANOVA Table

• H0 a1 ... ak 0 (m1 ... mk )
• HA Not all ai 0 (Not all mi are equal)

24
Example - Theophylline Interaction

• Goal Determine whether Cimetidine or Famotidine
  interact with Theophylline
• 3 Treatments Theo/Cim, Theo/Fam, Theo/Placebo
• 14 Blocks Each subject received each treatment
• Response Theophylline clearance (liters/hour)

Source Bachmann, et al (1995)
25
Example - Theophylline Interaction

• The test for differences in mean theophylline
  clearance is given in the third line of the table
  
• T.S. Fobs10.59
• R.R. Fobs ? F.05,2,26 3.37 (From F-table)
• P-value .000 (Sig. Level)

26
Example - Theophylline InteractionPost-hoc
Comparisons
27
Example - Theophylline InteractionPlot of Data
(Marginal means are raw data)
28
RBD -- Non-Normal DataFriedmans Test

• When data are non-normal, test is based on ranks
• Procedure to obtain test statistic
• Rank the k treatments within each block
  (1smallest, klargest) adjusting for ties
• Compute rank sums for treatments (Ti) across
  blocks
• H0 The k populations are identical (m1...mk)
• HA Differences exist among the k group means

29
Example - tmax for 3 formulation/fasting states

• k3 Treatments of Valproate Capsule/Fasting
  (i1), Capsule/nonfasting (i2),
  Enteric-Coated/fasting (i3)
• b11 subjects
• Response - Time to maximum concentration (tmax)

Source Carrigan, et al (1990)
30
Example - tmax for 3 formulation/fasting states
H0 The k populations are identical
(m1...mk) HA Differences exist among the k
group means